DM553 / MM850 - Computability and Complexity
Preface
Disclaimer: The notes presented here are mostly intended for use by me during exercise sessions. As such, they are often incomplete (not as detailed as a written assignment should be) and may contain simplifications / omissions that will be discussed during the exercise sessions. They may even contain unintentional errors.
During the corona epidemic, I will try to make my notes a bit nicer for the people staying at home. If you notice errors or have questions, feel free to send me an e-mail. Also, stay tuned for more information about how we will conduct exercise sessions remotely. This page can be found here exported as a pdf file.
Note 5
Problems for .
3.6
This exercise concerns theorem 3.21 which states that a language Turing-recognizable iff some enumerator enumerates it. We are to consider a wrong simplification of the proof in one direction; given TM, construct enumerator printing its language. Let \(s_1, s_2, \dots\) be all strings of \(\Sigma^*\)
- For \(i = 1,2,\dots\)
- Run \(M\) on \(s_i\) (original proof of 3.21: run \(i\) steps on each of \(s_1, s_2, \dots, s_i\))
- If accept, print \(s_i\)
Answer: the problem is that we don’t know that \(M\) will necessarily halt (only a recognizer). Thus, our constructed enumerator may get stuck if \(M\) loops.
3.13
Show: a language decidable iff there is an enumerator enumerating it in standard string order. Main point: consider when / why decidability is important here.
Answer:
- Decidable if enumerable in order
- We wish to construct a TM that will decide if an input string \(w\) is in the language of the enumerator
- Inspired by theorem 3.21, let the enumerator print out all strings of the language in standard string order
- Simulate this enumerator and every time it says to print a string \(s_i\), compare this to \(w\). Accept if equal.
- We also need to reject all strings not in the language. Due to knowing an ordering on the strings, we can tell if the strings output by the enumerator are suddenly “past” the input string. In this case (\(w \prec s_i\)), reject
- Enumerable in order if decidable: just like original proof. Enumerate all strings of \(\Sigma^*\) in order, run machine on each and print if accept.
3.17
Write-once TM: a TM which can only change symbol on each position on tape at most once. Show: this model of TM can do the same as a normal Turing machine can.
Hint: start out by considering write-twice TM and using a lot of tape.
Answer: let’s start with a way to simulate a normal TM in a write-twice TM. Idea: every time we would like to write to a cell for the second time, mark it instead. Then add a delimiter to the end of current tape contents, copy everything up to the mark, then write the replaced symbol and finally the rest of the old contents. This way, we can end up copying the entire content of the tape per write—but it works.
Now for the write-once version, we need to implement the marking without writing
twice. We can do this by using two fields per element instead of one such that
each copied symbol a is copied into _a and to mark it, write the mark on the
space. Have to adapt the machine such that it skips past these spaces when
reading (extra states in all transitions). Additionally, should modify machine
to use a new symbol where it would normally use the empty spaces.
One thing to note for both: consider how the copying could be implemented—using extra states or by extending the alphabet.
3.18
TM with doubly infinite tape: tape has no left endpoint. To prove: these recognize the class of Turing-recognizable languages.
Answer:
Suppose we have regular TM recognizing language. Then we create a doubly infinite one where we initially mark the square left of the input by \(\#\). All states get self-loop with \(\#,R\). We can now simulate the regular TM using a doubly-infinite one.
Note that by shifting input arbitrarily to the right (as needed), ordinary TM can emulate doubly-infinite TM. Put some marker on the left-most end of the tape and if we ever want to move further left, shift everything to the right first.
Alternative suggestions:
- Use multi-tape TM where tape 1 is starting point and everything to the right
while tape 2 is everything to the left of start in reverse order
- Have to make a copy of states with movement reversed on tape 2
- Have to detect when to switch between the two
- Considering how to implement multi-tape, this would look somewhat similar to above approach “in practice”
- Make clever mapping such that every odd-numbered \(n\) cell is \((n-1)/2\) on infinite tape while every even-numbered cell except the first one (could use a marker) is distance \((n-2)/2\) to the left of start.
3.20
TM with stay put instead of left: can go right or not move. Never goes to the left again. Show: not equivalent to normal TM, consider what can be recognized.
Answer:
Intuition: can probably recognize regular languages (have only states and no “memory” as it cannot move backward). It is trivial to prove that stay-put TMs can recognize at least the set of regular languages.
To show that they can only recognize regular, consider how to create an NFA from a stay-put TM (staying put is epsilon). Some care has to be taken if the TM stays while rewriting and changing states (note that doing so does not give it any useful “memory” and we can simulate this using extra NFA states).
Implementation details left to the reader. Main observation: as the TM has finite alphabet finite number of states, anything it can accomplish by standing still and writing to the same cell can be encoded in a finite number of states of an NFA (and of course, writing while moving to the right makes no difference when it cannot go back).
4.2
Consider problem of showing whether a DFA and a regular expression are equivalent. Formulate as language and show decidable.
Answer:
As a language:
\begin{equation*} \{\langle M, R\rangle\ \mid\ L(M) = L(R)\} \end{equation*}To determine language, we need to test if the DFA is equivalent to the regex. Recall the following facts:
- Can make DFA from regex
- Regular languages closed under intersection and complement (therefore also set difference)
- \(A=B \iff A \setminus B = B \setminus A = \emptyset\)
- We can decide if a given DFA will accept any string
This one is easy if you know theorem 4.4. Very easy if you know theorem 4.5 (then we only need step 1).
4.4
Show: language of CFGs which generate the empty string is decidable.
\begin{equation*} A_{\varepsilon\text{CFG}} = \left\{ \langle G \rangle\ \mid\ G \text{ is a CFG generating } \varepsilon \right\} \end{equation*}Answer: In the input, we will have the set of variables. We say that a variable is nullable if it can be rewritten to epsilon or a sequence of nullable variables. We can repeatedly go through all transitions, marking more variables nullable. If the starting variable becomes nullable, epsilon can be generated. If not and no changes are found in an iteration (finite number of variables, rules so this terminates), epsilon cannot be generated.
Short version: convert to Chomsky normal form (this does the whole nullability thing as part of the conversion) and check whether or not the starting variable can be rewritten to epsilon.
4.5
Show: \(\overline{E_{\text{TM}}}\) is Turing-recognizable.
Answer: Once again, consider all strings over \(\Sigma^*\): \(s_1, s_2, \dots\). We make a TM that, given \(\langle M \rangle\) as input will:
- for \(i = 1, 2, \dots\)
- simulate \(M\) on \(s_1, s_2, \dots, s_i\) for \(i\) steps
- if any of those simulations end in accept, then accept (the corresponding \(s_k\) proves that the language of \(M\) is not empty)
4.7
Show: this set is uncountable.
Answer: This exact example is illustrated nicely on Wikipedia. Given any enumeration \(s_1, s_2, \dots\) of these infinite strings, create a string which in position \(i\) differs for \(s_i\) at this position (swap 0 and 1 in this case). By construction, this string is not in the enumeration.
4.8
Show: this set is countable.
Answer: Recall the Cantor pairing function seen in the discrete math course to show that the set of rational numbers is countable. This sort of argument, we can just apply twice.
Or even better, recall (also from discrete math—we proved this via induction in an exercise) that the Cartesian product of finitely many countable sets is countable.
Note 6
Problems for .
4.11
We say that a variable \(A\) in CFG \(G\) is usable if it appears in derivation of some string \(w \in L(G)\). Problem: given \(G\) and \(A\), check if \(A\) is usable. Formulate as language, show it is decidable.
Answer: Language formulation omitted here. To decide:
- Variable must be reachable
- \(S\) is reachable
- If \(A\) is reachable and \(A \to s_1 B s_2\), then \(B\) is reachable
- Variable must derive terminals (let’s say it must be generating)
- All variables deriving terminals are generating
- If \(A \to BCD\) and \(BCD\) are all generating, \(A\) is generating
Both the sets (reachable and generating variables) can be computed by iterating over grammar a finite number of times. \(A\) must be in intersection.
Note: this is not quite enough. How can we avoid a false positive in the event that \(A\) is only reachable in a derivation where non-terminating variables are also produced?
4.13
Show: it is decidable.
Answer:
In case we are to check if \(L(G)\) is infinite: there will, for long enough strings, be some reuse of varialbes (think of pumping lemma proof). This comes from cyclic behavior in expansions. Check if any variable can derive itself (potentially via some intermediaries)—this can be done using a finite number of cycle-detection schemes.
In case \(k\) is finite, we can first make sure the language is actually finite using the approach just described. Now, to make sure that the number of strings of the finite language is exactly \(k\), we can exploit the fact that there will be a limit on the length of the strings we would need to check (refer to pumping lemma for rough upper bound). As such length is finite, we can enumerate and test all such strings (thm. 4.7 says that \(A_{\text{CFG}}\) is decidable). Can potentially lower the number of derivations to try, but this is not important.
4.16
From now on: in definitions, I probably omit stuff like “\(M\) is a DFA” because it’s usually implied (you should always write it in your assignments still).
\begin{equation*} PAL_{\text{DFA}} = \left\{ \langle M \rangle\ \mid\ M \text{ accepts some palindrome} \right\} \end{equation*}Show: it is decidable (hint is to use some theorems about CFLs).
Answer: We only need the following three ingredients:
- We can come up with a CFG generating all palindromes
- We can also intersect a context-free language with a regular language to get a context-free language
- Finally, \(E_{\text{CFG}}\) is decidable
4.21
Show:
- PREFIX-FREE(REX) is decidable (given regular expression, decide if its language is prefix free)
- How the same approach does not work to decide PREFIX-FREE(CFG)
Answer: convert regex to DFA. For one accepted string to be a prefix of another, the corresponding run through the machine (must be deterministic for this argument) goes from start to some accept to some (maybe even the same) accept again. So do some graph traversal:
- Which accept states are reachable from start?
- For each of these, can any accept state be reached?
If yes for any in the second case, then the language is not prefix-free.
Second part, PDA attempt at proof does not really work as traversing the digraph representation does not really cover the language properly. Not all CFGs even have a deterministic PDAs.
4.28
Show that the following is decidable:
\begin{equation*} \left\{ \langle G \rangle\ \mid\ 1^* \cap L(G) \neq \emptyset \right\} \end{equation*}Answer: Again, this is just a matter of recalling useful facts and theorems:
- Intersecting a context free language with a regular language gives a context free language
- \(1^*\) is regular, so \(1^* \cap L(G)\) is context free
- We know from thm. 4.8 that \(E_{\text{CFG}}\) is decidable
4.32
Show: can decide whether a given DFA generates an infinite language.
Answer: Digraph cycle idea: to recognize infinitely many strings, there must be some cycle and from (or on) the cycle, it must be possible to reach an accept state.
Language intersection idea: machine having \(n\) states can only accept strings of length \(\leq n-1\) without having to resort to cycles (refer to proof of pumping lemma).
- We can create DFA of all \(w \in \Sigma^*\) where \(|w| \geq n\)
- We can intersect it with input DFA
- We can check if resulting language is empty
- If no, original DFA generates strings long enough that language must be infinite
- If yes, original DFA had finite language
Brute force version: check all strings of length \(n \leq k < 2n\) (same purpose as intersection).
Note 7
Problems for .
5.3
Post Correspondence Problem, find match in:
\begin{equation*} \left\{ \begin{bmatrix}ab\\abab\end{bmatrix} \begin{bmatrix}b\\a\end{bmatrix} \begin{bmatrix}aba\\b\end{bmatrix} \begin{bmatrix}aa\\a\end{bmatrix} \right\} \end{equation*}Answer: I found
\begin{equation*} \left\{ \begin{bmatrix}ab\\abab\end{bmatrix} \begin{bmatrix}ab\\abab\end{bmatrix} \begin{bmatrix}aba\\b\end{bmatrix} \begin{bmatrix}b\\a\end{bmatrix} \begin{bmatrix}b\\a\end{bmatrix} \begin{bmatrix}aa\\a\end{bmatrix} \begin{bmatrix}aa\\a\end{bmatrix} \right\} \end{equation*}Or:
ab|ab|aba|b|b|a a|a a ab ab|aba b|b|a|a|a|a
5.4
Does \(A \leq_m B\) for regular \(B\) imply that \(A\) is regular?
Answer: No! Prove false using contradiction. Favorite non-regular yet context-free language: \(A = \left\{ a^ib^i\ \mid\ i \geq 0 \right\}\). Choice of \(B\) depends on the computable function we wish to construct.
\(B = \left\{ a \right\}\) is finite and therefore regular. Since \(A_{\text{CFG}}\) is decidable, the following is a computable function:
\begin{equation*} f(w) = \begin{cases} a & w \in A \\ b & \text{otherwise} \end{cases} \end{equation*}We see that \(w \in A \iff f(w)\) by construction, so \(A \leq_m B\). But \(A\) is not regular.
5.5
Show: \(A_{\text{TM}}\) not mapping reducible to \(E_{\text{TM}}\) (no computable function reduces the former to the latter).
Answer: Suppose it was mapping reducible via some computable function \(f\). Can use on complements (biimplication in definition);
\begin{equation*} w \in \overline{A} \iff f(w) \in \overline{B} \end{equation*}- We have shown that \(\overline{E_{\text{TM}}}\) is recognizable
- Corollary 4.23 states that \(\overline{A_{\text{TM}}}\) is not
- We get a contradiction via thm. 5.28 (\(A \leq_m B\) and \(B\) recognizable means \(A\) recognizable)
5.6
Prove: \(\leq_{m}\) is transitive. That is,
\begin{equation*} A \leq_m B \wedge B \leq_m C \implies A \leq_m C \end{equation*}Answer: Just write it out. We know there are two functions:
\begin{align*} w \in A & \iff f(w) \in B \\ w \in B & \iff g(w) \in C \end{align*}And we need to find \(h\) (actually, TM computing \(h\)) such that:
\begin{equation*} w \in A \iff h(w) \in C \end{equation*}We construct TM for \(h\) as follows: given some input \(w\):
- run \(M_f\), leaving \(w' = f(w)\) on tape
- run \(M_g\), leaving \(w'' = g(f(w))\) on tape
So \(h = g \circ f\) and by definition of \(f\) and \(g\), we know that \(w \in A \iff w'' \in C\).
5.9
Show: undecidable. Hint: use Post Correspondence Problem (book shows reduction strategy—not depicted here).
Answer: we just want to argue that the reduction presented in the book is valid. That is, the PCP instance generated has a match if and only if the grammar is ambiguous.
Suppose the PCP instance has a match. Consider the ordered multiset giving same string above and below. Can use this to get derivation sequences in grammar. Same strings generated via \(T\) and \(B\) (\(a_i\) only relevant for other direction of proof).
Suppose CFG is ambiguous. Note that the \(a_i\) are new, unique and always at the end of strings, so any string derived from \(T\) is “unique” in this part of the grammar. To generate the same string via \(B\) (only way to get ambiguity), we have to get some \(b\) strings to match the \(t\) strings—but the \(a\) parts ensure that the \(t\) and \(b\) parts used come from matching pairs in the PCP instance.
5.10
Show: \(A\) is Turing-recognizable iff \(A \leq_m A_{\text{TM}}\).
Answer: Important: just have to show recognizable and not decidable.
Suppose \(A\) is Turing-recognizable. Take machine \(M_A\) recognizing \(A\). The following computible function is trivial: \(f(w) = \langle M_A, w \rangle\).
- If \(w \in A\), then \(f(w) \in A_{\text{TM}}\)
- If \(f(w) \in A_{\text{TM}}\), then \(w \in A\)
Thus \(A \leq_m A_{\text{TM}}\).
Suppose now that \(A \leq_m A_{\text{TM}}\) (want to show that \(A\) is recognizable). Take the function \(f\) computed by \(M_f\) where we know:
\begin{equation*} w \in A \iff f(w) \in A_{\text{TM}} \end{equation*}We know taht \(A_{\text{TM}}\) is recognizable, so can compute \(f(w)\) recognize if \(f(w) \in A_{\text{TM}}\) and therefore \(w \in A\).
5.11
Show: \(A\) decidable iff \(A \leq_m 0^* 1^*\).
Answer:
Suppose \(A\) decidable, show reducible. Because \(A\) is decidable, the following function is computable:
\begin{equation*} f(w) = \begin{cases} \varepsilon & w \in A \\ 10 & w \notin A \end{cases} \end{equation*}Second case just needs to be not in \(0^*1^*\). Observe that by construction, \(f\) is a reduction function.
Suppose reducible, show decidable. Consider reduction function \(f\) which is computable. To decide, given any \(w\), whether \(w \in A\), just:
- Compute \(f(w)\)
- Check if \(f(w) \in 0^*1^*\) (trivial)
- If yes, accept
- If no, reject
5.16
Prove Rice’s theorem. \(P\): nontrivial property of language meaning it contains some but not all TM descriptions. And:
\begin{equation*} L(M_1) = L(M_2) \implies (\langle M_1 \rangle \in P \iff \langle M_2 \rangle \in P) \end{equation*}(membership of \(P\) depends only on language of TM)
Answer: Proof is tricky, here is annotated version: assume for contradiction decidable for some \(P\) and use this to decide \(A_{\text{TM}}\). Assume \(M_{\emptyset}\) (where \(L(M_{\emptyset}) = \emptyset\)) is not in \(P\). We can take some \(M_P \in P\) because \(P\) is nontrivial. Now, given some \(\langle M, w \rangle\):
- Create a TM \(M'\) which does the following when given \(x\) as input:
- Simulate \(M\) on \(w\), reject if it rejects
- Note that this may loop
- If always looping or rejecting, \(L(M') = \emptyset\)
- Simulate \(M_P\) on \(x\), accept if it accepts
- Simulate \(M\) on \(w\), reject if it rejects
- Use decider for \(P\) to decide if \(\langle M' \rangle \in P\), accept if it is (reject otherwise)
The point of this construction is that \(\langle M'\rangle \in P\) if and only if \(\langle M, w\rangle \in A_{\text{TM}}\).
Suppose the constructed \(\langle M' \rangle \in P\). This means that \(M'\) gets past the part where it simulates \(M\) on \(w\) (if it didn’t, the language would be empty as it would reject / loop on any \(x\)) to simulate \(M_P\) on \(x\).
Suppose now that \(\langle M, w \rangle \in A_{\text{TM}}\). This means that \(M'\) gets to simulate \(M_P\) on \(x\) which means that \(\langle M' \rangle \in P\) by construction (could also do contraposition here).
5.18
Use Rice’s theorem to prove some languages undecidable.
a
Answer: Rice’s theorem applies:
- Some TMs have infinite languages, others don’t (give examples). Therefore, this is not a trivial property.
- Two machines with the same language will also have same language cardinality, so one is included iff the other is included. Therefore, this property is a property of the languages of TMs.
Since the two conditions for Rice’s theorem are fulfilled, we can use the theorem and thus conclude that INFINITE is undecidable.
Let’s expand on these two things we need to show to use Rice’s theorem. First, the property has to be non-trivial. That is, it contains some Turing machines, but not all. For instance, the following boring TM will accept any string and definitely have an infinite language (it is therefore in INFINITE):
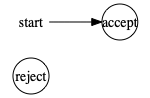
On the other hand, this TM will reject all strings and so not have an infinite language (and is therefore not in INFINITE):
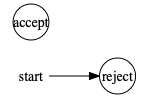
The second condition is:
\begin{equation*} L(M_1) = L(M_2) \implies (\langle M_1 \rangle \in P \iff \langle M_2 \rangle \in P) \end{equation*}If \(L(M_1)=L(M_2)\), then \(|L(M_1)|=|L(M_2)|\). Suppose \(M_1\) has an infinite language—then \(M_2\) does, too, and they are both in INFINITE. If \(M_1\) does not have an infinite language, then neither does \(M_2\) and neither of them are in INFINITE.
b
Answer:
- Some TMs have the language of only
1011(can construct one), others don’t (also easy to construct) - If \(L(M_1) = L(M_2)\), then it is obvious that the property applies to both or none
c
Answer:
- Some TMs have the language \(\Sigma^*\) (can construct one), others don’t
- If \(L(M_1) = L(M_2)\), then it is obvious that the property applies to both or none
5.28
Show that the following problem is undecidable (formulate as language first): does a given single-tape TM ever write the blank symbol over a nonblank symbol for any given input string?
Answer: as a language
\begin{equation*} A = \left\{ \langle M \rangle\ \mid\ \exists x \in \Sigma^*: \text{when run on $x$, $M$ writes blank over non-blank symbol} \right\} \end{equation*}Suppose for contradiction this is decided by TM \(M_A\). Then we can decide \(A_{\text{TM}}\): given \(\langle M, w \rangle\),
- Create a TM \(M'\)
- Simulate slightly modified \(M\) on \(w\)
- We don’t want this simulation to write blank over non-blank; can avoid this by carefully replacing blank character writes during simulation with some new symbol
- If it accepts, write blank over some non-blank symbol (can write non-blank first to have something to overwrite in case there is nothing)
- Simulate slightly modified \(M\) on \(w\)
- Simulate \(M_A\) on \(M'\), accept if it accepts (reject otherwise)
By construction, \(M'\) will write the blank symbol on a non-blank cell if and only if \(M\) accepts \(w\).
Note 8
Discuss on /.
5.29
In a TM: a useless state is a state that is never encountered on any input string. Formulate as language the problem of determining whether a TM has any useless states and show that this is undecidable.
Answer: As a language, this problem is
\begin{equation*} \text{USELESS}_{\text{TM}} = \left\{\langle M\rangle\ \mid \text{ $M$ is a TM containing a useless state}\right\} \end{equation*}where one might add that a useless state \(q\) means
\begin{equation*} \nexists s \in \Sigma^*: \text{ $M$ enters $q$ when run on $s$} \end{equation*}We will be reducing from \(A_{\text{TM}}\). Plan: given \(\langle M, w \rangle\), make a TM where accept state is useless iff \(M\) does not accept on \(w\). This \(M'\) should just reject on any \(w' \neq w\). Then, when run on \(w\), we want to make sure that, when rejecting, it uses all states except accept. Otherwise, one of the other states could be useless—and we only want accept to potentially be useless.
We can get it to visit all states except accept by introducing a new character on the tape and adding transitions on this character that form a tour of the states. In the machine I describe below, this tour should end in the reject state.
So, suppose \(M_U\) decides USELESS. Create new \(M'\) which given \(\langle M, w \rangle\) will:
- Create new \(M''\) based on \(M\) which takes input \(x\):
- All transitions to reject state are replaced by tour to every non-accept state before rejecting
- If \(x \neq w\), then reject
- Otherwise run as normal on \(x\)
- Now, run \(M_U\) on \(M''\)
- If it accepts, then accept state was useless and so reject
- If it rejects, then all states were useful (including accept), so accept
Think about: why do we not need to do tour before accepting? Could we structure the machine (including when to do a tour) differently?
34.1-3
Describe how to formally encode an arbitrary digraph as binary string as an adjacency matrix and as an adjacency list.
Answer:
- Adjacency matrix
- Need \(n \times n\) matrix
- Can give \(n\) in unary via 1s (end with 0) to avoid having to worry about word length
- Knowing \(n\), we can just list the \(n^2\) entries with 0 or 1
- Adjacency list
- Can again give \(n\) (necessary?)
- For each node:
- Give number of outgoing arcs (could be in unary)
- Then give ID for each target (could be in in unary; then, each ID would be long number separated by 0)
34.1-5
Show: if an algorithm makes at most constant calls to poly-time subroutines and does poly-time additional work, then the algorithm is poly-time. Also: show polynomial number of calls to polynomial-time subroutines may give exponential-time algorithm.
Answer: First, simply observe that:
\begin{equation*} c \cdot n^{k_1} + n^{k_2} \in O\left( n^{\max\{k_1,k_2\}} \right) \end{equation*}Now, suppose we have some algorithm polynomial in its input:
poly(n):
for i=1 to n
do something uninteresting
Now, we make an algorithm calling it polynomially many times:
notsopoly(n):
m = 1
for i=1 to n
m = m*2
poly(m)
Observe that the final call will have the value \(m=2^n\), so the poly-time
algorithm will do work that is exponential in the value of \(n\) as seen by
notsopoly.
34.2-3
Show: if HAM-CYCLE is in P, then we can list vertices of such a cycle in order in poly-time. Keep in mind: HAM-CYCLE only tells us whether a hamiltonian cycle exists in the graph. Problem is to extract (and sort) it.
Answer: We assume that there is a Hamiltonian cycle (at least one) in the graph before starting (otherwise there is nothing to do). Idea: throw out edges until only such a cycle remains. Given \(G=(V,E)\):
- for each \(e \in E\)
- \(G' = (V, E \setminus \{e\})\)
- call HAM-CYCLE on \(G'\)
- if there is still a cycle in \(G'\):
- \(G \gets G'\)
This is polynomially many calls to HAM-CYCLE and afterwards, \(G\) will only contains edges on such a Hamiltonian cycle. Using any graph traversal we choose, starting at any vertex, we can now list the vertices of \(G\) in the order the cycle visits them.
Note exercise about poly-time
Suppose: have language \(L\) and algorithm accepting string \(x \in L\) in poly-time, but rejecting \(x \notin L\) in super-polynomial time. Show: can then decide \(L\) in polytime.
Answer: if we know a (possibly rough) polynomial \(n^k\) bound for the running time in case \(x \in L\), then we can simply run the given algorithm for that amount of time (number of steps). If it has not accepted by then, we can safely reject.
Also, note that on pages 1059-1060 in Cormen, the proof of theorem 34.2 is essentially stating this exact argument.
34.2-4
Prove: NP closed under regular operations. In all situations, we have two languages with each their own verification machines.
Answer:
Union: Here, we have two “obvious” options. One is (like with union for Turing-decidable languages) to simply take as certificate a certificate from either of the two languages and run both verification machines on it, accepting if either one does so. The other is to let the certificate be a flag indicating which of the two languages a given string belongs to and based on this, run the corresponding verifier.
Intersection: Try to verify using verifier for both languages. If both accept, accept. Since the two verifiers may have different certificates, we should define certificates for the intersection such that the certificates needed by both machines are included—simplest way would be to concatenate them with an indication of which part belongs to which original certificate.
Concatenation: Combine two certificates with some marker to indicate where to split input string. Then run each machine on each part and accept if both do.
We are supposed to skip Kleene star.
34.2-8
\(\phi\) is a boolean formula over variables \(x_1, x_2, \dots, x_k\). Has \(\neg\), \(\wedge\), \(\vee\) and \(()\). The language TAUTOLOGY is the language of all such formulae which are tautologies. Show that TAUTOLOGY is in co-NP (that is, the complement of TAUTOLOGY is in NP)..
Answer: Suppose we have \(\phi\) which is not a tautology. This means that for some assignment of truth values to variables in \(\phi\), \(\phi\) is false. Given this assignment and \(\phi\), it is trivial to verify that \(\phi\) can, indeed, be falsified (just insert the values and evaluate).
34.3-6
Show: Only \(\emptyset\) and \(\{0,1\}^*\) are not complete in P wrt. poly-time reductions.
Recall: \(L_1 \leq_p L_2\) iff there is poly-time computable \(f: \{0,1\}^* \to \{0,1\}^*\) s.t.:
\begin{equation*} x \in L_1 \iff f(x) \in L_2 \end{equation*}Answer: Suppose we have a \(L_2\) which is neither empty nor every possible string. Then there is some string \(a \in L_2\) and string \(b \notin L_2\). Take any \(L_1\) from P; the following function is trivially computable in poly-time (as \(L_1\) is in P):
\begin{equation*} f(x) = \begin{cases} a & x \in L_1 \\ b & x \notin L_1 \end{cases} \end{equation*}This approach obviously does not work for \(\emptyset\) and \(\{0,1\}^*\) because it is not possible to use them to “distinguish”.
Note 9
Discuss on .
Find error in an argument
Algorithm for finding factors of a number: given input \(n \in \mathbb{N}\), do
- for \(i=2\) to \(n-1\)
- if \(i\) divides \(n\), output \(i\)
- if nothing output, output \(-1\)
Claim that checking whether a number divides another in \(O(log^3 n)\) time:
- multiplication can be done in \(O(\log^2 n)\) on binary representation of \(n\)
- could use binary search \(O(\log n)\) steps to find \(k\) s.t. \(ik=n\)
So total running time of algorithm to find factors is \(O(n \log^3 n)\). Why does this not break RSA?
Answer: consider what the “input size” for our problem is. The time arguments made rely on the value or magnitude of \(n\). However, input size is not the same as the value of the single number \(n\).
It would probably be expressed as a binary number where the input size would be number of bits; the magnitude of the number would then be exponential in the “size of the input”.
Make formula false
Consider a formula with exactly three literals per clause. We want to add a constant number of three-literal clauses that will make any such formula false.
Answer: just choose (or add) three arbitrary literals and add the eight clauss consisting of every different regular / negated version of them:
\begin{align*} (x \vee y \vee z) & \wedge (x \vee y \vee \neg z) \wedge (x \vee \neg y \vee z) \wedge (x \vee \neg y \vee \neg z) \wedge \\ (\neg x \vee y \vee z) & \wedge (\neg x \vee y \vee \neg z) \wedge (\neg x \vee \neg y \vee z) \wedge (\neg x \vee \neg y \vee \neg z) \end{align*}34.2-5
Show: any language in NP could be decided by algorithm running in \(2^{O\left(n^k\right)}\) where \(k\) is some constant.
Answer: Idea by certificates: by definition of NP, any yes-instance has poly-length certificate which can be checked in poly-time. We can enumerate certificates and try them.
Let’s be more formal. On page 1064 of the textbook, the definition is that \(L\) is in NP iff there is a polynomial-time algorithm \(A\) and constant \(c\) such that:
\begin{equation*} L = \left\{ \begin{split} x \in \{0,1\}^*:\ &\text{ there exists a certificate $y$ where $|y| \in O(|x|^c)$}\\ &\text{ such that $A(x,y)=1$} \end{split} \right\} \end{equation*}There will be \(2^{O(n^c)}\) certificates to try and \(A\) runs in polynomial time, say bounded by \(O(n^{a})\).
- \(2^{O(n^c)}\) certificates
- Each of length \(O(n^c)\) thus taking time \(O((n^c)^a) = O(n^{ca})\) to run \(A\) on one
- For a total of \(2^{O(n^c)} \cdot O(n^{ca})\) time to try them all
Setting a sufficiently large \(k\), the total time is definitely bounded asymptotically by \(2^{O(n^k)}\). A quick choice could be \(k=2ca\).
34.2-10
Prove: if NP \(\neq\) co-NP, then P \(\neq\) NP.
Answer: We will use our favorite proof method: contraposition. Suppose P equals NP. This would mean that, for any problem in NP, we can find a solution in poly-time (decider). Then consider the complement; we can just check if any given instance is in the original language and answer in the negative of the result (P is closed under complement due to argument like an exercise from last time). So then P=NP=co-NP.
34.3-7
Prove: \(L\) is complete for NP wrt. poly-time reductions iff \(\overline{L}\) is complete for co-NP.
Answer: Suppose \(L\) is complete in NP. Recall that this means that for any \(L'\) in NP, there is a function \(f\) where \(x \in L' \iff f(x) \in L\). We can just take complements;
\begin{equation*} x \notin L' \iff f(x) \notin L \equiv x \in \overline{L'} \iff f(x) \in \overline{L} \end{equation*}Observe that this is a polynomial reduction from \(\overline{L'}\) which is in co-NP to \(\overline{L}\). This goes both ways, so \(\overline{L}\) is complete in co-NP.
Going right-to-left is just a matter of playing the equivalences / biimplications backwards.
34.4-4
Show: determining if boolean formula is tautology is complete in co-NP. Hint: use exercise 34.3-7 which asks to prove that \(L\) is complete in NP iff \(\overline{L}\) is complete in co-NP.
Note: we have previously shown that TAUTOLOGY is in co-NP (34.2-8).
Answer: Let’s call the complement of TAUTOLOGY FALSIFIABLE. Can make poly-time reduction from SAT to FALSIFIABLE (claim), so FALSIFIABLE is complete in NP. Via 34.3-7, we conclude then that TAUTOLOGY is complete in co-NP.
To expound on the claim that SAT can be reduced to FALSIFIABLE: recall that an instance of SAT is a formula \(\phi\) and the goal is to determine if it can be satisfied. Note that any assignment that makes \(\phi\) true will make \(\neg \phi\) false—so our reduction is simply negating the formula, knowing that \(\neg \phi\) will be in FALSIFIABLE if and only if (since it will be due to the same assignment) \(\phi\) is in SAT.
34.4-5
Show: determining satisfiability of formula in DNF is poly-time solvable.
Answer: Since the formula is in DNF, we only need to satisfy one clause. For each clause, try to assign values to satisfy it—there is only one way to do so, if any. If a clause proves to be a contradiction, just move along to the next one. If any satisfiable clause is found, we have satisfying (partial) assignment. Else, no solution exists.
34.4-6
Suppose: we have poly-time algorithm for SAT. How to find concrete assignment in poly-time?
Answer: Assume that the formula is initially satisfied (otherwise this is boring).
- start with empty assignment; \(f(x) := ?\) for all variables \(x\)
- for each variable \(x\):
- assign to true; setting \(f(x) := \text{true}\)
- meaning we modify the formula such that each occurrence of \(x\) is replaced by “true”
- if we don’t want to have “true” in the formula, the modification could be done equivalently by removing occurrences of \(x\) along with any parts satisfied by \(x\)
- if the modified formula is still satisfiable, this was a correct (or irrelevant) assignment
- if however the modified formula is now unsatisfiable, set instead \(f(x) :=
\text{true}\)
- note that the formula modified according to this must be satisfiable again
- assign to true; setting \(f(x) := \text{true}\)
When this terminates (in case we remove satisfied parts, it may terminate early when the remaining formula is empty), \(f\) is a (maybe partial) assignment satisfying the formula.
34.4-7
Consider 2-CNF-SAT. Show that it is in P. Make efficient algorithm. Use \(x \vee y \equiv \neg x \implies y\) and reduce the problem to efficiently solvable digraph problem.
Answer:
Digraph version: make \(D=(V,A)\) where \(V\) consists of all variables in regular and negated form. \(A\) is then implications. Observe that \(D\) has size polynomial in the size of the formula.
The \((x \vee y) \equiv (\neg x \implies y) \equiv (\neg y \implies x)\) implications (now represented as arcs) each means that if \(\neg x\) is true, then \(y\) has to be true, too. As only one of \(x\) and \(\neg x\) can be true, cycles would be a problem. If there is a cycle containing any variable and its negation, then there cannot be a satisfying assignment.
Below, the digraph representing \(\neg x \vee y\), \(\neg y \vee z\), \(\neg z \vee \neg y\), and \(y \vee x\) is shown as an example. Arcs colored red and blue for “symmetric” arcs: for \(\neg x \vee y\), the arc \(x \to y\) is blue and \(\neg y \to \neg x\) is red.
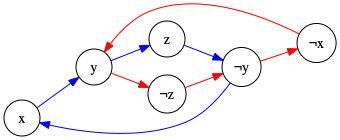
Note that there is clearly cycles between both regular and negated vertices for the same variables; for instance \(x \to y \to \neg z \to \neg y \to x\). To verify for yourself that this formula cannot indeed be satisfied, observe the following truth table:
| x | y | z | ¬x∨y | ¬y∨z | ¬z∨¬y | y∨x |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Now, to find an algorithm to check this. Naive approach: for each variable, see if there is path to its negation (could use DFS) and back again. This would be \(\Theta(n(n+m))\). Could use Floyd-Warshall to achieve this in \(\Theta(n^3)\) and then if for any \(x\), distance from \(x\) to \(\neg x\) is finite and \(\neg x\) to \(x\) is, too.
If we know how to find SCCs: In a strongly connected component, there can be no solution iff any \(x\) and its corresponding \(\neg x\) are in the same SCC (by above argument, all literals / vertices in the same SCC have the same value). After building graph, find all SCCs in \(O(m+n)\) and check if any variables have both nodes in same SCC. With some consideration, we could do each such check in constant time and thus stay in \(O(m+n)\).
Note 10
Discuss on .
34.5-1
Recall definition of isomorphic (as it pertains to graphs). \(G_1\) and \(G_2\) are isomorphic if there exists a bijection \(f: V_1 \to V_2\) on the vertex sets such that for all \(v_i, v_j \in V_1\), \((v_i, v_j) \in E_1 \iff (f(v_i), f(v_j)) \in E_2\).
Show: subgraph-isomorphism problem NP-complete. The problem is, given \(G_1\) and \(G_2\) to determine if \(G_1\) is isomorphic to a(n induced) subgraph of \(G_2\).
Answer: Just have to think of a suitable well-known NP-complete graph problem to use. Let’s make a reduction from CLIQUE.
- Clique instance: \(G=(V,E), L\) and the question is whether there is a clique of size \(L\) in \(G\)
- We create a subgraph-isomorphism instance \(C_L, G\)
- \(G\) is the original graph from CLIQUE (we clearly want to find something in this graph)
- \(C_L\) is a clique of size \(L\) that we simply construct
Finding \(C_L\) in \(G\) is exactly finding a clique of size \(L\), so correctness of the reduction is pretty trivial.
Just to make sure that the reduction is polynomial: we only need to consider \(|C_L| \leq |G|\). That is, if \(L > |V|\) or if \(\frac{L(L-1)}{2} > |E|\), we can just answer no instead of creating \(C_L\) at all.
From note: find an isomorphism
Assume we have a poly-time algorithm solving the subgraph-isomorphism (decision) problem. Use this to find an isomorphism.
Answer: First, we can remove unnecessary nodes from second graph (remove one at a time, add if it removes all mappings). Secondly, we need to determine a bijection between the two vertex sets remaining.
Silly (yet polynomial) strategy: individualize vertices by adding a unique subgraph outside (maybe just a clique of size \(n+1\)) and connecting to only one node on both sides.
Faster (but to me less obviously correct): remove vertex in second graph one at a time. For each one, find the corresponding vertex in first graph by removing one at a time here.
34.5-2
Show: 0-1-integer programming problem NP-complete via reduction from 3-CNF-SAT.
Answer:
Let \(A\) have dimensions \(m \times n\) where \(m\) is number of clauses and \(n\) is number of variables. The 0/1-vector \(x\) will have \(n\) entries, each representing a variable (0 for false, 1 for true).
Each row in \(A\) models a clause; it has only 3 non-zero entries (one for each literal appearing in the clause). These non-zero entries are 1 for negated variables and -1 for regular ones. The corresponding row in \(b\) will have value equal to number of negated variables minus one.
Example: \((\neg x_1 \vee x_2 \vee x_3)\) will in \(A\) appear as \(1\ -1\ -1\). Looking in the truth table below, the row with 100 (making this clase false) is bad and causes has sum 1 where it shoudl be \(\leq 0\). All others fine and have sum \(\leq 0\).
| x1 | x2 | x3 | sum |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | -1 |
| 0 | 1 | 0 | -1 |
| 0 | 1 | 1 | -2 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | -1 |
From note: also reduction from vertex cover
Try reduction from vertex cover to 0-1-integer programming. Instance of vertex cover is graph \(G=(V,E)\) and number \(k\), asking whether a cover \(C \subset V\) exists where \(|C| \leq k\). Note: the cover covers all edges, that is \(\forall \{u,v\} \in E: u \in C \vee v \in C\).
Answer: Here, \(A\) can have dimensions \(m \times n\) such that each row represents an edge (has two non-zero entries indicating endpoints). If endpoints are -1 and \(x\) has entries 1 for each selected node, then each entry of \(b\) is just -1.
Problem: resolve the problem that this only gives a vertex cover. What about guaranteeing that it has size something? Idea: add an extra row which counts the number of selected vertices. Row should have all ones. Corresponding entry in \(b\) should be \(k\).
Note 11
Dicussed on . Handwritten notes from exercise session here.
34.5-4
Show: if target value of subset-sum problem is given in unary, the problem can be solved in poly-time. Look at pages 1128-1129 for a hint.
Recall: a subset-sum problem instance is a pair \((S,t)\) where \(S\) is a set of positive integers \(\{x_1, \dots, x_n\}\) and \(t\) is a positive integer. Question is whether there exists a subset of \(S\) summing to exactly \(t\).
Answer: the point in this exercise is that the target value expressed in unary will have magnitude polynomial in input size (well, equal to, pretty much). The book (following the hint) gives an “exponential-time” exact algorithm. It is exponential because the lists \(L_i\) can reach length up to \(2^i\). However, as we are dealing with positive integers, we don’t really care about lists longer than \(t\) as they will include elements greater than \(t\) (and so would be thrown away anyway).
So we could just use the merge-list-based exact sum algorithm from the book because this is polynomial in the value of the target \(t\). In fact, the book mentions this already; the algorithm is polynomial-time in case \(t\) is polynomial in \(|S|\) or all numbers in \(S\) are polynomially bounded by \(|S|\).
Also: Any pseudopolynomial solution will be polynomial in this setting. Example: dynamic programming solution which takes time \(O(sn)\) where \(s\) is sum to hit.
numbers = [1,5,6,13,14] target = 20 # Q[i][j]: can sum of subset of S[:i] be j? Q = [[False for j in range(target+1)] for i in range(len(numbers))] for i in range(len(numbers)): val = numbers[i] Q[i][0] = True # can always hit 0 for j in range(1, target+1): Q[i][j] = \ (val == j) or \ Q[i-1][j] or \ (j>=val and Q[i-1][j-val]) print(Q[-1][-1])
True
34.5-5
Show: set-partition problem is NP-complete.
Instance is \(S\) which is just a set of numbers. Question is whether \(S\) can be partitioned into two sets such that each of these two sets has the same sum.
We are allowed to redefine set partition to allow the same value to appear more than once.
Answer:
Trivial part: argue it is in NP. Omitted here.
Reduction from subset-sum. Consider subset-sum instance:
\begin{equation*} A=\{a_1,a_2,\dots,a_n\}, t \in \mathbb{N}. \end{equation*}Let \(S = \sum_{i=1}^{n}a_i\). Create then an instance \(A' = A \cup \{S - 2t\}\) of set partition. We now prove this is a valid reduction (given: it is polynomial).
Suppose there exists a subset \(B \subseteq A\) s.t. \(\sum B = t\) (solution to subset sum). Then,
\begin{align*} \sum(A \setminus B) &= S-t \text{ and }\\ \sum (B \cup \{S - 2t\}) &= S-t, \end{align*}so there exists a satisfying partition.
Suppose there is a satisfying partition. Each must have sum \(S-t\) by construction. One of the parts, \(B'\) will contain the element \(S-2t\). Removing this element, we see that \(\sum(B' \setminus \{S-2t\}) = t\), so we have the subset sum solution right there.
Reduction found in old notes: choose some \(w > \max\{S,t\}\) and use partition instance \(A \cup \{w-t, w-S+t\}\) (generalization).
34.5-6
Show: hamiltonian-path problem is NP-complete. Recall: hamiltonian path is just a simple path visiting each vertex exactly once (like HAM-CYCLE, but path instead of cycle).
Answer:
Trivial: it is in NP. Reduction from HAM-CYCLE instance \(G=(V,E)\):
- for each \(e \in E\):
- create new graph without this edge, \(G' = (V, E\setminus \{e\})\)
- for the two endpoints, add new nodes with only connections to these
endpoints such that any path ham-path will start/end here
- \(e = \{u,v\}\)
- add nodes \(s_u\) and \(s_v\) to \(G'\)
- add edges \(\{s_u,u\}\) and \(\{s_v,v\}\) to \(G'\)
- if there is a HAM-PATH \(p\) in \(G'\), there was a HAM-CYCLE \(p \setminus \{\{s_u,u\},\{s_v,v\}\} \cup \{e\}\) using the removed edge in the original graph (and vice versa)
34-2
We consider a bunch of variations on problems involving a bag of money to be divided between Bonnie and Clyde. For each problem, either show that it is NP-complete or give a poly-time algorithm.
- a
Bag contains \(n\) coins, but only two different denominations \(x\) and \(y\). Have to divide the money evenly.
Answer:
This problem is in P. Could probably solve it quickly with a clever algorithm, but even silly brute force works and is poly-time: suppose \(n_1\) coins have value \(x\) and \(n_2\) have \(y\). Let the goal (half) be \(t:=xn_1+yn_2\).
- for \(i=0 \dots n_1\)
- for \(j = 0 \dots n_2\)
- if \(i x + j y = t\)
- return true
- if \(i x + j y = t\)
- for \(j = 0 \dots n_2\)
- return false
Note: polynomial (even with the multiplication stuff) because each element is already listed in input (the operations are polynomial in the representation we are given).
Note also: polynomial for any constant number of different denominations.
- for \(i=0 \dots n_1\)
- b
Bag contains \(n\) coins of arbitrarily many denominations—but all denominations are powers of two.
Answer:
This problem is in P. Let half of total sum be \(t\) again.
- while \(t > 0\)
- if any remaining coins have value \(v < t\)
- let \(x\) be the biggest of these coins
- \(t \gets t - x\)
- remove \(x\) from bag
- else return false
- if any remaining coins have value \(v < t\)
- return true
Argument to make: biggest power of two not greater than remaining part is in solution (easier to argue in recursive formulation). If it is given to Bonnie and Clyde cannot get enough (smaller) coins in any way, then there was no solution. If Clyde can get at least the same amount in (not greater) coins, then a subset of these have the same value as the big one.
- while \(t > 0\)
- c
Bag contains \(n\) checks with arbitrary amounts on them.
Answer: NP-complete. This is obviously the set-partition problem in disguise.
- d
Bag contains \(n\) checks, but Bonnie and Clyde are okay with an unfair split; difference must be at most 100 dollars.
Answer: NP-complete. By blowing up values of set-partition by a factor of more than 100, the answer would be the same. Blowup is polynomial.
34-3
Working with graph coloring. An instance is \(G\) and it is minimization problem (minimum number of colors). Will end up showing that the decision problem 3-COLOR is NP-complete.
- a
Find 2-coloring efficiently if one exists.
Answer: Just do DFS or BFS (any traversal will do) and keep alternating between two colors. If a conflict is detected, then there really was no solution anyway (cycle of odd length is detected).
- b
Cast the graph-coloring problem as a decision problem and show it is equivalent to regular graph-coloring (that is, the minimization version minimizing number of colors used).
Answer:
As decision problem: is there a \(k\)-coloring? Given a graph \(G=(V,E)\) and a number \(k\).
Now, to show that it is poly-time solvable iff graph coloring (finding minimum number of colors) is. It is trivial that solving minimization version allows solving decision version. The other way around, we find the minimum number by just trying:
- for \(i = 0 \dots n\)
- if \(G\) admits an \(i\)-coloring
- return \(i\)
- if \(G\) admits an \(i\)-coloring
- for \(i = 0 \dots n\)
- c
3-COLOR: language of graphs which admit 3-colorings. Show: if NP-complete, then decision problem from b is, too.
Answer: Simply observe that 3-COLOR is special case \(k=3\) of the decision problem we just gave.
- d
Read reduction from 3-CNF-SAT to 3-COLOR and start explaining why it works. Given a formula, create graph with following vertices:
- One vertex for each variable and one for each variable negated
- Five vertices for each clause (explained later)
- Three special vertices, TRUE/FALSE/RED (constant)
And the following edges:
- Clause edges follow from widget later (related to the five vertices per clause)
- Literal edges form triangles:
- The three special vertices are in one
- Each variable \(x\) has \(x\), \(\neg x\) and RED as triangle
Now argue: any 3-coloring \(c\) on the graph with only the literal edges means that, for each variable \(x\), only one out of the vertices representing \(x\) and \(\neg x\) will have the same color as TRUE (the other one shares color with FALSE).
Then argue: for any truth assignment (consistent), there is a 3-coloring on graph with just literal edges.
Answer: Look at the literal edges for the three special vertices and one pair representing some variable \(x\):
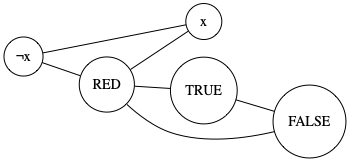
The first point we should argue is obvious by the construction; because \(\neg x\), \(x\), and RED form a triangle, each of them will have different colors. Because RED, TRUE, and FALSE form a triangle, so will they—so \(x\) will have the same color as either TRUE or FALSE while \(\neg x\) will have the other remaining color.
Noting that the triangles only intersect on RED, it is easy to 3-color the graph. Not much to show for the second argument.
- e
Argue that the widget given by figure 34.20 in the book works: it should be 3-colorable if and only if at least one of \(x,y,z\) is colored true (corresponding to a clause \((x \vee y \vee z)\)).
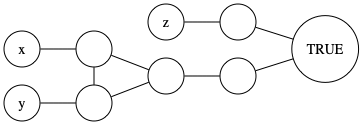
Answer: If all three are colored false, then there is no 3-coloring. Check for 1/2/3 colored true that a 3-coloring can be found. Important to keep the literal edges in mind when checking this.
- f
Prove: 3-COLOR is NP-complete.
Answer:
Technically, we should first note that it is in NP in the first place. This is trivial.
Now, we have the construction for the reduction from 3-SAT. It is polynomial in size. Literal edges enforce consistency, clause edges mean that there exists a 3-coloring iff there exists a satisfying assignment.
Note 12
Discussed on . Handwritten notes from exercise session here.
1. 3.10 from notes
Show: can find median of five elements using six comparisons in worst case.
Answer:
Start by comparing two pairs of elements. Suppose a<b and c<d. Then, compare the two losers; suppose a<c. We can discard a now.
We have now b (bigger than one element), c (smaller than one, bigger than one), d (bigger than one) and e (uncompared). We compare b with e and have two cases:
- b<e means we have two “chains” a<c<d and a<b<e
- compare and wlog assume c<b (symmetric)
- now a<c<d and a<c<b<e means only d or b can be median; take the smaller one
- compare and wlog assume c<b (symmetric)
- b>e means we have (a,e)<b and a<c<d
- compare e with c, giving two cases
- e<c means (a,e)<b and (a,e)<c<d so only b, c remain as candidates; take smaller one
- e>c means a<c<d and a<c<e<b, leaving d,e as candidates; take smaller one
- compare e with c, giving two cases
2. Lower bound on merging
Have sorted lists of length \(n\) and \(m\), wish to merge. Prove (tight) lower bound of \(n+m-1\).
Answer:
Consider final list of length \(n+m\). If only \(n+m-2\) comparisons were used, there must be a pair of consecutive elements which were not compared. Suppose these came from two different lists (can create input so this happens); we can then run the algorithm again where they should be from same list and as the algorithm cannot distinguish, it will be wrong in one case.
3.a Baase: consecutive zeros in a string
Question is: does a given bit string contain two consecutive zeros? For sizes of 2 to 5, give either an adversary algorithm forcing any algorithm to query every bit or give an algorithm that is correct without querying all bits.
Answer:
- n=2 obvious adversary: say 0 first (have to check the other)
- n=3 almost obvious adversary
- if 2 is queried, answer 0 (from here, obvious)
- if 1 or 3 is queried, answer 1 and proceed with n=2 strategy
- n=4 has algorithm querying only 3 bits, starting with 2
- if
_1__, we can ignore index 1 and proceed with 3,4 (3 checks in total) - if
_0__, query index 3- if
_00_, done - if
_01_, we can ignore 4 and need only check 1 (3 checks in total)
- if
- if
- n=5 has clever adversary; for any query, we give response
- if 1 is queried, answer 0
0____01___reduces to n=30_1__reduces to n=2 and 2 must be queried0__0_can force all to be queried (answer 1)0___101__1reduces to n=20_0_1remaining must be queried (answer 1)0__01ditto
- if 2 is queried, answer 0
_0___10___101__n=2 remaining10_0_both remaining must be queried (answer 1)10__0ditto
_01__already covered (will always set 1 to 1)_0_0_ditto
- if 3 is queried, answer 1
__1__- this reduces to two cases of n=2 where adversary is known
- if 1 is queried, answer 0
3.b Baase: finding one of the smallest keys
Algorithm
Have \(n\) keys and integer \(1 \leq k \leq n\). Have to find one of the \(k\) smallest keys. Idea: naive linear minimum algorithm on the first \(n-k+1\) elements using \(n-k\) comparisons.
Lower bound
Suppose we could find it in \(n-k-1\) comparisons. Can then make adversary make us give \(n-k-1\)’st key which is wrong. With \(n-k-1\) comparisons, we know that \(n-(n-k+1)\) subsets of elements have not been compared to each other (think of Hasse diagrams). Therefore, the adversary can choose to say that whichever element we select—even if it is minimum of some subset—is \(k+1\)’th instead of among \(k\) smallest.
4. Baase: kth-smallest in sorted arrays
L1 and L2 are arrays. Each has \(n\) keys and is sorted. Find the \(k\)’th smallest element.
Give an algorithm
\(O(\log n)\) by doing alternating divide and conquer / binary search.
- let x be median element (in middle) of L1
- do binary search for x in L2, let i be index of smallest element greater than x
- if \(n/2+i = k\), return x (maybe off by one)
- if \(n/2+i > k\), recurse with L2[:i], L1[:n/2], k
- else recurse with L2[i:], L1[n/2:], k-n/2-i
Can improve to \(O(\log k)\) by noting that we only care about up to first \(k\) elements of each
Give a lower bound
Information theoretic bound: there would be \(2n\) (or \(2k\)) leaves in decision tree, giving a depth of \(\Omega(\log n)\) (\(\Omega(\log k)\)).
5. Finding third largest in array
Naive way: use maximum finder three times; first two times discarding maximum. This would take \(n-1+n-2+n-3=3n-6\) comparisons.
Could also: maintain top three all the time. Worst case involves swapping each time. Would require \(0+1+2+3(n-3)=3n-6\) comparisons.
6. Sorting by reversals
Algorithm
Suppose we just:
- for i=1 to n
- find minimum of A[i:] with index j
- reverse interval [i,j]
This way we do at most n-1 reversals
Lower bound
Consider the sequence 1 3 5 7 ... n-1 2 4 6 8 ... n.
- For n=4 or above, no number has correct neighbour
- A reversal changes neighbours for at most 4 numbers
- At least \(n/4\) reversals must be performed
Why can’t we use ordinary lower bound?
Algorithm is not analyzed in decision tree model under comparisons.
Note 13
Discussed . Handwritten notes from exercise session here.
Note 14
Discussed . Handwritten notes from exercise session here.
Note 15
Discussed . Handwritten notes from exercise session here.
Note 16
Discussed . Handwritten notes from exercise session here.
Note 17
Discussed on . Handwritten notes from exercise session here.
Note 18
Discussed on . Handwritten notes from exercise session here.
Note 19
Discussed on . The example solutions for assignment 3 can be found here.
Example solution to assignment 3
This is intended to serve as an example solution for the assignment. It includes the details I would look for in a thorough answer. Note that this is by no means perfect: it could definitely be more concise and I have included comments that are not strictly necessary (only there to point out that there are more details one could consider).
Problem 1
For the regular “Cave Tunnels” (CT) problem, an instance has the form \((G=(V,E), k)\) where \(G\) is the graph corresponding to the given map of tunnels: \(V\) is the set of rooms with \(|V|=n\) and \(\{u,v\} \in E\) if the rooms \(u\) and \(v\) are connected by a tunnel. The regular CT problem is to find the maximum number of tunnels which can be controlled by placing \(k\) blockers on nodes of the given graph.
a
To get a decision problem, we add a target value. An instance of “Decide Cave Tunnels” (DCT) consists of \((G, k, t)\) and the question is whether the \(k\) blockers can be placed on rooms of \(G\) such that at least \(t\) tunnels are controlled.
We first show that DCT is in NP. Suppose a certificate is given which indicates which rooms to place blockers in; that is, some \(S \subseteq V\) with \(|S| = k\). It is then trivial to verify in polynomial time that there are at least \(t\) tunnels present in \(E\) connecting rooms in \(S\)—this could for example be done by querying \(E\) for each of the \({|S| \choose 2}\) potential edges.
We now show that DCT is complete in NP by providing a reduction from the known NP-complete problem CLIQUE (theorem 34.11 in Cormen). Given an instance \((G, k)\) of CLIQUE, construct an instance of DCT of the form \(\left( G, k, t={k \choose 2} \right)\). That is, the same graph is used and we will argue that there exists a clique of size \(k\) in \(G\) if and only if \(k\) blockers can be placed such that they control \(t\) tunnels.
Suppose there is a clique of size \(k\) in \(G\). Placing all \(k\) blockers on the vertices of this clique will yield a solution where all tunnels (edges) among rooms (vertices) of the clique are controlled. As a clique is by definition a complete (sub)graph, there will be exactly \({k \choose 2} = t\) controlled tunnels.
Suppose now that here is a way to place \(k\) blockers on a subset \(S\) of \(G\) with \(|S|=k\) such that \(t\) tunnels are controlled. As both endpoints of a tunnel must be blocked for a tunnel to be controlled, all the \(t\) controlled tunnels are between rooms in \(S\). The largest possible number of controlled tunnels must therefore be \({|S| \choose 2}=t\), requiring \(S\) to be a complete (sub)graph. This means that \(S\) is indeed a clique of size \(k\).
This concludes the proof of the correctness of the reduction. As the value of \({k \choose 2}\) can be computed in polynomial time, this is a polynomial-time reduction.
b
We will now show how a polynomial-time algorithm for DCT would allow us to construct a polynomial-time algorithm for the evaluation version, CT. The input is \((G, k)\) and the goal is to find \(t^{\star}\), the maximum number of tunnels that can be controlled using \(k\) blockers. The algorithm is simply:
- for \(t=1\) to \({k \choose 2}\):
- run the decider for DCT on \((G, k, t)\)
- if it accepts, continue
- if it rejects, return \(t-1\)
By construction, this algorithm will return the largest number \(t^{\star}\) of tunnels which could be controlled by \(k\) blockers. Assuming \(k \leq n\),
\begin{equation*} {k \choose 2} = \frac{k(k-1)}{2} \leq \frac{n(n-1)}{2} \in O(n^2) \end{equation*}means that the loop will have a polynomial number of iterations and thus a polynomial number of calls to the decider for DCT (note that even if \(k>n\), the decider would reject at \(t>{n \choose 2}\) assuming \(G\) is a simple graph).
c
We now show that a polynomial-time decider for DCT can be used to find a concrete placement of blockers maximizing the number of controlled tunnels. Again, let the input be \((G, k)\). Below, \(G'-e\) refers to the graph attained by removing \(e\) from the edges of \(G'\) (leaving the nodes unchanged).
First, use the algorithm from (b) to find \(t^{\star}\). Then:
- Set \(G' = G\) and \(S = \emptyset\).
- for \(e \in E\):
- run decider for DCT on \((G'-e, k, t^{\star})\)
- if it (still) accepts, let \(G' \gets G'-e\)
- if it rejects, let \(S \gets S \cup e\) (where \(e=\{u,v\}\))
- return \(S\)
After running this algorithm, \(G'=(V,E')\) will contain a minimal set of edges for which it holds that \(k\) blockers could control \(t^{\star}\) edges. As this set is minimal, there is an optimal solution where all of \(E'\) is controlled and thus \(|E'| = t^{\star}\). Additionally, the set of their endpoints of \(E'\) is \(S\) and must have cardinality \(k\).
The algorithm uses a polynomial number of iterations and the input graphs given to DCT are of non-increasing size, so still clearly polynomial in the original input size.
Instead of finding the set of tunnels controlled in an optimal solution, the same approach could be applied to the vertices to iteratively find the set of rooms to place the blockers in. This would require at most \(n\) calls to the DCT decider.
d
Graphs of degree at most two can only be composed of simple paths and cycles. We consider only graphs consisting of either a path or a cycle. We are allowed to assume that the input graph is connected.
Consider an instance \((G, k, t)\) of DCT where \(G\) is a simple path of length \(n\). As both endpoints of a tunnel must be blocked to control the tunnel, the optimal placement of blockers on a path must clearly be to block consecutive rooms; the first two blockers control one tunnel and every additional blocker will control another tunnel. The decision problem for a path can then be solved trivially for a path in polynomial time since exactly \(k-1\) (for \(k \leq n\)) tunnels can be controlled: simply answer whether \(k-1 \geq t\).
Consider now an instance \((G, k, t)\) of DCT where \(G\) forms a simple cycle. For
\(k
As it is trivial using graph traversal to determine which of the two cases applies, we now have an algorithm which decides DCT for graphs of maximal degree 2 in polynomial time. If DCT is still NP-complete for maximum degree 2, then this would imply that \(P=NP\). Assuming \(P \neq NP\) implies that DCT for maximum-degree 2 is no longer NP-complete.
In extending the algorithm to general (not necessarily connected) graphs of maximum degree two, one non-trivial issue is how to optimally cover some subset of cycles as covering a cycle entirely is always a better use of blockers than only partially covering cycles or entirely covering paths. This problem can be solved in polynomial time using dynamic programming, but as we are allowed to assume that the input graph is connected, we omit the details of this here.
Problem 2
Out of \(n\) people, \(2k\) have a virus and we need to find \(k\) of them.
a
To identify and test \(k\) infected, consider the naive approach of testing one person at a time:
- \(I = \emptyset\)
- for each person in arbitrary order:
- test if this person is infected; if they are, add them to \(I\)
- if \(|I| = k\), return \(I\)
As there will be exactly \(n-2k\) non-infected persons in the population, this algorithm will at most test \(n-2k+k = n-k\) persons before having identified a set \(I\) of exactly \(k\) infected.
To establish a matching lower bound, suppose an algorithm could identify \(k\) infected persons using at most \(n-k-1\) tests. An adversary algorithm could answer that the first \(n-2k\) tests were all negative and the last (at most) \(k-1\) tests performed were positive. Thus, the algorithm has found and tested at most \(k-1\) infected people and is therefore not correct.
b
We now allow algorithms to—based on knowing \(n\) and \(k\) ahead of time—deduce the set of infected people without necessarily testing them. The naive algorithm can then be changed to:
- \(I = \emptyset\), \(S = \emptyset\)
- for each person in arbitrary order:
- test if this person is infected;
- if they are, add them to \(I\)
- if they are not, add them to \(S\)
- if \(|I| = k\), return \(I\)
- if \(|S|=n-2k\), return any subset of \(k\) people in \(\overline{S}\)
- test if this person is infected;
The difference is that now identifying all the \(n-2k\) non-infected persons will let us immediately conclude that the remaining are infected in which case no more tests are needed. At most, this approach will test \(n-2k-1\) non-infected persons, \(k-1\) infected persons and then one additional person (infected or non-infected) before terminating. This is in total up to
\begin{equation*} n-2k-1 + k-1 + 1 = n-k-1 \end{equation*}tests.
This immediately gives the adversary algorithm proving a matching lower bound. Suppose an algorithm uses at most \(n-k-2\) tests. An adversary could answer that the first \(n-k-1\) people tested were non-infected and the remaining at most \(k-1\) tested were infected. There will be at least \(k+1\) untested people remaining and at least one of them is not infected. The algorithm has only decidedly identified \(k-1\) infected, so it must include at least one of the \(k+1\) untested as its output—the adversary can simply answer that this person is (among the) last non-infected people.
Problem 3
For the information-theoretic lower bound, we ignore the people with the \(k\) highest identification numbers (these are assigned before the algorithm runs and not related to infection status).
We model all algorithms as binary decision trees in which each node corresponds to testing one person at a time (branching on whether or not the test is positive). We know from the slides that a \(t\)-ary tree with \(n\) leaves has height \(\left\lceil \log_t(n) \right\rceil\). The height of the decision tree will correspond to the number of tests performed in the worst case to reach a leaf corresponding to a result.
We thus need to count how many leaves the decision tree must have. The population to consider has size \(n-k\) and—depending on the input and which are ruled out by having the highest IDs—any subset of size \(k\) could be the correct answer. This leads to \({n-k \choose k}\) possible outputs or leaves. The straightforward lower bound achieved this way will therefore be:
\begin{equation*} \left\lceil \log_2 {n-k \choose k} \right\rceil = \left\lceil \log_2 \frac{(n-k)!}{k!(n-2k)!} \right\rceil \end{equation*}Footnotes:
Note that if \(k \geq n\) and \(t > k \geq n\), then the instance could be seen to be a no-instance already by the fact that \(t\) is strictly greater than the number of tunnels.