DM811 - Heuristics for Combinatorial Optimization
Sheet 3, Autumn 2010 [pdf format]

Prepare the following exercises for discussion in class on Friday December 3.

Exercise 1

Definition 1  The Max Weighted Independent Set Problem

Given: an undirected graph G(V,E) and a non-negative weight function ω on V (ω : V → R)

Task: A largest weight independent set (aka, stable set) of vertices, i.e., a subset V′ ⊆ V such that no two vertices in V′ are joined by an edge in E.

Related problems:

Definition 2  Vertex Cover

Given: an undirected graph G(V,E) and a non-negative weight function ω on V (ω : V → R)

Task: A smallest weight vertex cover, i.e., a subset V′ ⊆ V such that each edge of G has at least one endpoint in V′.

Definition 3  Maximum Clique

Given: an undirected graph G(V,E)

Task: A maximum cardinality clique, i.e., a subset V′ ⊆ V such that every two vertices in V′ are joined by an edge in E

Note also that the independent set problem is equivalent to the set packing problem and the vertex cover problem is a strict special case of set covering problem.

Exercise 2

Definition 4  Single Machine Total Weighted Tardiness Problem

Input: A set J of jobs {1,…,n} to be processed on a single machine and for each job j ∈ J a processing time pj, a weight wj and a due date dj.

Task: Find a schedule that minimizes the total weighted tardiness ∑j=1n wj · Tj, where Tj={Cj−dj,0} (Cj completion time of job j).

Is the problem NP-hard? If the problem is NP-hard, design at least one construction heuristic and at least one local search (solution representation + neighborhood + evaluation function).

Exercise 3

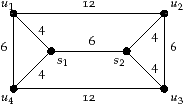
The Steiner tree problem is a generalization of the minimum spanning tree problem in that it asks for a spanning tree covering the vertices of a set U. Extra intermediate vertices and edges may be added to the graph in order to reduce the length of the spanning tree. These new vertices introduced to decrease the total length of the connection are called Steiner1 vertices.

Definition 5  Steiner Tree Problem

Input: A graph G=(V,E), a weight function ω: E ↦ N, and a subset U ⊆ V. Task: Find a Steiner tree, that is, a subtree T=(VT,ET) of G that includes all the vertices of U and such that the sum of the weights of the edges in the subtree is minimal.

The example in Figure 1 is an instance of the Euclidean Steiner problem showing that the use of Steiner vertices may help to obtain cheaper subtrees including all vertices from U.

Figure 1: Vertices u1, u2, u3, u4 belong to the set U of special vertices to be covered and vertices s1,s2 belong to the set S of Steiner vertices. The Steiner tree in the second graph has cost 24 while the one in the third graph has cost 22.


  1. Design one or more local search algorithms for the Steiner tree problem. In particular, define the solution representation and the neighborhood function.
  2. Provide an analysis of the computational cost of the basic operations in the local search algorithms designed at the previous point. In particular, consider the size of the neighborhood, and the cost of evaluating a neighbor.

Exercise 4

Definition 6  Total Weighted Completion Time on Unrelated Parallel Machines Problem

Input: A set of jobs J to be processed on a set of parallel machines M. Each job j ∈ J has a weight wj and processing time pij that depends on the machine i ∈ M on which it is processed.

Task: Find a schedule of the jobs on the machines such that the sum of weighted completion time of the jobs is minimal.

  1. Design a local search algorithm by defining the solution representation and the neighborhood function.
1
Jakob Steiner (18 March 1796 – April 1, 1863) was a Swiss mathematician.