DM825 - Introduction to Machine Learning
Sheet 10, Spring 2011 [pdf format]

Exercises 1.29, 1.30, 14.3, 14.1, 14.6, 14.11 of [B1].

Check exercise 14.11. Here is the vresion from the Errata Corrige:

1  Exercise 1 – Tree based methods

You are given the following data points: Negative: (-1, -1) (2, 1) (2, -1); Positive: (-2, 1) (-1, 1) (1,-1). The points are depicted in Figure 1.

---

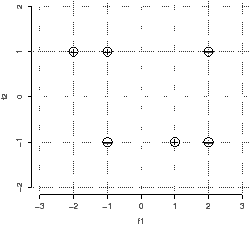
Figure 1: The data points for classification.

---

1. Construct a decision tree using the greedy recursive bi-partitioning algorithm based on information gain described in class. Use both criteria the Gini index and the entropy. In the search for the split threshold θ discretize the continue scale of the two features and consider only values in {−1.5,0,1.5} for f₁ and {0} for f₂. Represent graphically the tree constructed and draw the decision boundaries in the Figure 1. Table 1 might be useful for some computations

   ---

   x	y	−(x/y) · log(x/y)	x	y	−(x/y) · log(x/y)
   1	2	0.50	1	5	0.46
   1	3	0.53	2	5	0.53
   2	3	0.39	3	5	0.44
   1	4	0.50	4	5	0.26
   3	4	0.31

   Table 1: Numerical values for the computation of information gains.

   ---

2. Use the tree to predict the outcome for the new point (1,1).

2  Exercise 2 – Nearest Neighbor

1. Draw the decision boundaries for 1-Nearest Neighbor on the Figure 1. Make it accurate enough so that it is possible to tell whether the integer-valued coordinate points in the diagram are on the boundary or, if not, which region they are in.
2. What class does 1-NN predict for the new point: (1, 1).
3. What class does 3-NN predict for the new point: (1, 0).