DM825 - Introduction to Machine Learning
Sheet 8, Spring 2011 [pdf format]

Exercise 1 Bayesian Networks – Inference.

Figure  shows a graphical model with conditional probabilities tables about whether or not you will panic at an exam based on whether or not the course was boring (“B”), which was the key factor you used to decide whether or not to attend lectures (“A”) and revise doing the exercises after each lecture (“R”).

You should use the model to make exact inference and answer the following queries:

• what is the probability that you will panic or not before the exam given that you attended the lectures and revised after each lecture?
• what is the probability that you will panic or not before the exam?
• your teacher saw you panicking at the exam and he wants to work out from the model the reason for that. Was it because you did not come to the lecture or because you did not revise?

Repeat the inference in the last two queries by means of stochastic inference implementing in R the Prior-Sample, Rejection-Sampling, Likelihood-weighting and Gibbs-Sampling Markov Chain Monte Carlo.

---

[ place/.style=ellipse,draw=black!50,fill=black!20,thick, inner sep=0pt,minimum size=1cm, pre/.style=<-,shorten <=1pt,>=angle 60,semithick, post/.style=->,shorten >=1pt,>=stealth’,semithick, transition/.style=rectangle,draw=black!100,fill=black!20,thick, inner sep=0pt,minimum size=3mm] [place] (b) at (1,4) B; [place] (r) at (0,2) R edge [pre] (b); [place] (a) at (2,2) A edge [pre] (b); [place] (p) at (1,0) P edge [pre] (r) edge [pre] (a); [left,minimum height=2cm, minimum width=2cm] (b2) at (b.west) 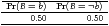; [left,minimum height=2cm, minimum width=2cm] (r2) at (r.west) ; [right,minimum height=2cm, minimum width=2cm] (a2) at (a.east) ; [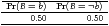left,minimum height=2cm, minimum width=2cm] (p2) at (p.west) ;

Figure 1: The graphical model of exercise 1. Lower-case letter indicate the outcome that the upper-case letter can take.

---

Exercise 2 Directed Graphical Models Consider the graph in Figure left.

• Write down the standard factorization for the given graph.
• For what pairs (i, j) does the statement X_i is independent of X_j hold? (Don’t assume any conditioning in this part.)
• Suppose that we condition on {X₂, X₉}, shown shaded in the graph. What is the largest set A for which the statement X₁ is conditionally independent of X_A given {X₂, X₉} holds?
• What is the largest set B for which X₈ is conditionally independent of X_B given {X₂, X₉} holds?
• Suppose that I wanted to draw a sample from the marginal distribution p(x₅) = Pr[X₅ = x₅]. (Don’t assume that X₂ and X₉ are observed.) Describe an efficient algorithm to do so without actually computing the marginal.

---

[ place/.style=ellipse,draw=black!50,fill=white,thick, inner sep=0pt,minimum size=0.5cm, placeb/.style=ellipse,draw=black!50,fill=black!20,thick, inner sep=0pt,minimum size=0.5cm, pre/.style=<-,shorten <=1pt,>=angle 60,semithick, post/.style=->,shorten >=1pt,>=stealth’,semithick, transition/.style=rectangle,draw=black!100,fill=black!20,thick, inner sep=0pt,minimum size=3mm] [place] (1) at (0,2) 1; [placeb] (2) at (0.5,1) 2; [place] (7) at (2.5,2) 7; [place] (8) at (4,2) 8; [place] (6) at (1,2) 6 edge [pre] (1) edge [pre] (2); [place] (10) at (1,0) 10 edge [pre] (2); [place] (4) at (1.5,1) 4 edge [pre] (6) edge [pre] (2) edge [pre] (7); [place] (3) at (2,0) 3 edge [pre] (10); [placeb] (9) at (2.5,1) 9 edge [pre] (7) edge [pre] (8) edge [pre] (3); [place] (5) at (3,0) 5 edge [pre] (9);

Figure 2: A directed graph.

---