DM828 - Introduction to Artificial Intelligence Exercise Sheet 6, Autumn 2011 [pdf format]

Exercises

The game tree in Figure 1 is limited to depth 3. The evaluation function values at this level are indicated. Assuming that the player at level 0 is MAX, at level 1 is MIN, at level 3 is MAX and at level 4 is MIN, perform the following algorithms:

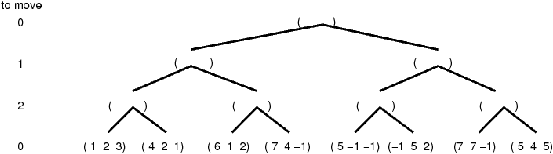
Minimax.
Left-to-right alpha-beta pruning.
Right-to-left alpha-beta pruning.

For the two alpha-beta pruning, indicate the direction you are taking, the alpha and beta values at the nodes ([α,β]), and exactly where pruning takes place (use a bar transversal to the pruned edge).

Consider now the situation in which the outcome of some actions is stochastic and all outcomes are equally likely. Perform:

Expectimax, assuming at level 0 there is a MAX player, at level 1 chance, at level 2 again MAX and at level 4 chance.
Expectiminimax, assuming at level 0 there is a MAX player, at level 1 chance, at level 2 MIN, at level 4 chance.

[level 1/.style=sibling distance=40mm, level 2/.style=sibling distance=20mm, level 3/.style=sibling distance=10mm, min/.style=isosceles triangle,draw=black!50,fill=black!20,thick, inner sep=0pt,minimum width=0.6cm, minimum height=0.5cm, shape border rotate=270, isosceles triangle stretches, max/.style=isosceles triangle,draw=black!50,fill=black!20,thick, inner sep=0pt,minimum width=0.6cm,minimum height=0.5cm,shape border rotate=90, isosceles triangle stretches, terminal/.style=rectangle,draw=black!50,fill=black!20,thick, inner sep=0pt,minimum width=0.5cm,minimum height=0.5cm] [circle=2pt,fill] child [fill] circle (2pt) child [fill] circle (2pt) child [fill] circle (2pt) node[below=2pt] 2 child [fill] circle (2pt) node[below=2pt] 3 child [fill] circle (2pt) child [fill] circle (2pt) node[below=2pt] 5 child [fill] circle (2pt) node[below=2pt] 9 child [fill] circle (2pt) child [fill] circle (2pt) child [fill] circle (2pt) node[below=2pt] 0 child [fill] circle (2pt) node[below=2pt] 1 child [fill] circle (2pt) child [fill] circle (2pt) node[below=2pt] 7 child [fill] circle (2pt) node[below=2pt] 4 child [fill] circle (2pt) child [fill] circle (2pt) child [fill] circle (2pt) node[below=2pt] 2 child [fill] circle (2pt) node[below=2pt] 1 child [fill] circle (2pt) child node (v) edge from parent[draw=none] child [fill] circle (2pt) node[below=2pt] 5 child [fill] circle (2pt) node[below=2pt] 6 child node (v) L=4 edge from parent[draw=none] child [grow=up] node (t) L=2 edge from parent[draw=none] child [grow=up] node (u) L=1 edge from parent[draw=none] child [grow=up] node (v) L=0 edge from parent[draw=none] ;
Figure 1: A game tree

Get aquainted with Kalaha reading the rules of the game and play a couple of games: http://kalaha.krus.dk/. Solve then by pen and paper the case with two pits for opponent and 2 stones within each pit. Consider then the more challenging case 6x6. How many search states there are? How would you implement efficiently the representation of a state? How would you implement a move generator? What could be a good scoring system? Provided alpha-beta search remains infeasible for this case, how would you proceed? Would iterative deepenining be a good strategy to apply? If yes or not, why? Be as deatiled in your explanation as possible.

Consider the following 2-player game. Cookies are laid out on a rectangular grid n× m. The cookie in the top left position is poisoned, as shown in Figure 2. The two players take turns making moves; at each move, a player is required to eat a remaining cookie, together with all cookies to the right and/or below it (see Figure 2, for example). The loser is the player who has no choice but to eat the poisoned cookie.

Draw the search tree for this game in a 3× 3 grid expanded by the left-to-right alpha-beta pruning algorithm. (Do not draw unexpanded subtrees.)

Is this game a fair or an impartial game? That is, can one of the players always make moves that are guaranteed to lead to a win if he starts? Does the conclusion changes if n≠ m?

Figure 2: A sequence of moves in the game of Exercise 1 starting with a 3× 5 grid. Player A must eat the last block and so loses.

The following code from the python aima repository implements the MIN-MAX algorithm for two-players games.

def minimax_decision(state, game):
    player = game.to_move(state)

    def max_value(state):
        if game.terminal_test(state):
            return game.utility(state, player)
        v = -infinity
        for (a, s) in game.successors(state):
            v = max(v, min_value(s))
        return v

    def min_value(state):
        if game.terminal_test(state):
            return game.utility(state, player)
        v = infinity
        for (a, s) in game.successors(state):
            v = min(v, max_value(s))
        return v

    # Body of minimax_decision starts here:
    action, state = argmax(game.successors(state),
                           lambda ((a, s)): min_value(s))
    return action

Let’s consider a three-player game (without alliances) and let’s call 0, 1, 2 the three players. Each terminal state has now associated three values indicating the likelihood of winning of player 0, 1 and 2, respectively.

a) Does the code above implement a MIN-MAX algorithm also for the three-player game? If not what has to be changed?
b) Complete the game tree of Figure 3 by filling the backed-up value triples for all remaining nodes.

Figure 3: The game tree of Exercise 2.

Exercise 5.16 of the text book.