FF505/FY505 – Computational Science
Week 7, Spring 2015 [pdf format]

MATLAB Exercises

Work in pairs at the following exercises with the help of MatLab.

  1. Read the slides from lecture 3 on Graphics. You do not have to memorize those things but it is good for you to know about their existence.
  2. Find the easiest way to plot a segment between two points both in 2D and 3D knowing the coordinates of the points.
  3. Show in a plot the trend of computation time as a function of the size of the matrix for the operations described in ex. 3 of Set 1. Vary the size of the matrix at intervals from 200 to 1000. You can add repetitions at each size and errorbars in the plot. Report the curves of the two methods (x=A \ b and y=inv(A)*b) in the same plot. Try log-transformations until the curves resemble a line. (Find size of matrices that allow to see differences in the results, alternatively make a loop in which the same operation is repeated several times, then the time for performing the operation once is the average time.)
  4. Draw the graphs of some partial sums for the Fourier series of f(x)=x3−3π/2x2, and compare these with the graph of f(x).
  5. Linear Transformations The cross product can be used to rotate three dimensional vectors. A rotation R is a linear operation characterized by a rotation axis n, and by a rotation angle φ. Let r be an arbitrary 3D vector and R(r) be its image under the rotation R. Then,
    R(r) = r +n × (n × r ) ( 1−cos(φ) ) +( n × r ) sin(φ),     (1)
    where × indicates the cross product.
    1. How many real numbers do you need to specify a rotation in 3D?
    2. The matlab program rotate.m produces Fig. 1. Read the script and understand what it is doing. Modify the program to produce similar figures with different rotation axes.
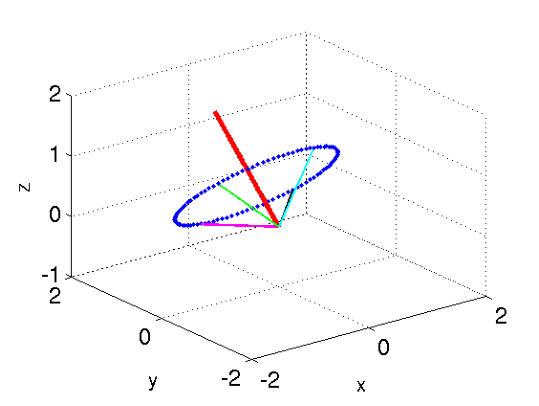
      Figure 1: The figure is obtained using Eq. 1. The thick axis is the rotation axis.
    3. Find the matrix of R in the standard basis.
    4. Here we only introduce and use the definition: v is a (right) eigenvector of the matrix L if and only if it satisfies the equation
      L v = λ v,     (2)
      where λ is a scalar.

      Show that the rotation axis n is an eigenvector of the rotation operator. What ts the corresponding eigenvalue? Give a physical interpretation.

  6. Numerical methods for Ordinary Differential Equations The study of population dynamics deals with the evolution of population of plants, animals or humans over time. The interest is answering questions about the asymptotic stability of the dynamic system, that is, for example, whether a specie will eventually become extinct.

    An important model in this field is the logistic equation or Verhulst equation

    y′=y−y2,    y(0)=0.2

    that expresses the rate of growth of the population y over time t (dy/dt=y′). The first term on the right hand side, y, determines a positive growth. If the model was just y′=y then the growth would be exponential and unlimited (you can verify this claim by deriving the solution of the equation). The second term, −y2, is a “braking term” that prevents the population from growing without bound. Finally, y(0) is the initial value, needed to solve the equation.

    The logistic equation above is a nonlinear nonhomogeneous ordinary differential equation (ODE) (see Chapter 1 of [Kr] for an explanation of these terms). That specific equation can be reduced to a linear form and the solution written down as a formula (that is, in closed form). If you do not remember or do not know how to derive the closed form of that equation, you can read on page 30 of [Kr].

    However, often a closed form is not known. Computational methods have then been developed for a numerical solution of the equation. More specifically, in MatLab there is a set of functions for carrying out this task in the case of ODEs. To gain an idea of the algorithms they implement you can read Section 21.1 of [Kr]. A distinction is done between stiff and nonstiff functions. The name is taken from one of the main applications of ODEs, which is in the study of oscillations. It is related to the value of the constants involved in the ODE. The term stiff recalls a mass-spring system with a stiff spring (large constant k). For stiff functions methods must be more accurate in order to avoid an increase in errors from the initial value.