Linear Systems of Equations

by Jarno Markku Olavi Rantaharju

System 1
System 2
System 3

System 1

2x + 2y = 1
6x + 3y = 3

To plot the equations using the plot function we first solve for y:

y = -x + 0.5, y = -2x + 1

Next we create a set of points (x,y). First define the points x

x1 = 0.1*[0:100] ;

and calculate y at each x

y1 = -x1 + 0.5 ;

repeat for the second equation

x2 = 0.1*[0:100] ;
y2 = -2*x2 + 1 ;

and plot both sets of points

plot(x1,y1,x2,y2)

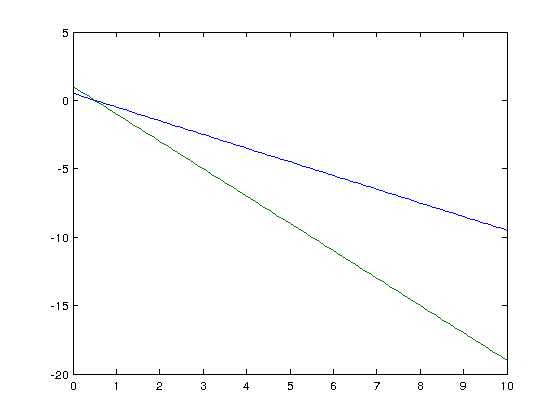
The equation should have exactly one solution. Lets look at the determinant. First, input the linear system as a matrix and a vector

A = [2,2;6,3]
b = [1;3]

The determinant of A is nonzero:

det(A)

ans =
    -6

This means that there is and inverse

inv(A)

ans =
   -0.5000    0.3333
    1.0000   -0.3333

and the solution is

inv(A)*b

ans =
    0.5000
         0

System 2

2x + y = 1

6x + 3y = 3

Again, first plot. Solve for y

y = -2*x + 1 y = -2*x + 3

Create the points (x,y) to plot

x1 = 0.1*[0:100] ;
y1 = -2*x1 + 1 ;
x2 = 0.1*[0:100] ;
y2 = -2*x2 + 3 ;

and make the plot

plot(x1,y1,x2,y2)

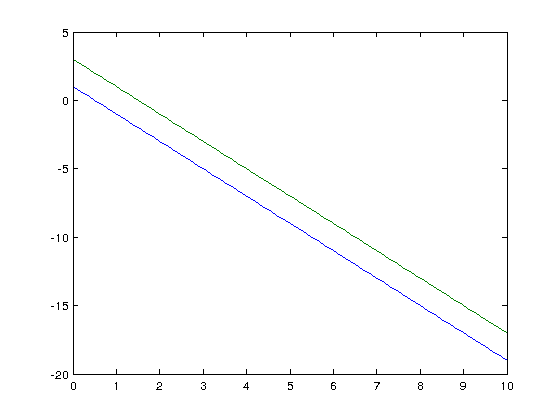
Now there are no solutions. In this case the determinant should be zero. Input the matrix and the vector

A = [2,1;6,3]
b = [1;2]

and the determinant is

det(A)

ans =
     0

If we try to solve the system, we get infinities

A\b

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate.
RCOND =  9.251859e-18. 
ans =
   1.0e+15 *
   -3.0024
    6.0048

System 3

x + 2y = 2

2x + 4y = 4

Plot first. Solve for y

y = -x/2 + 2

Now create the points (x,y)

x1 = 0.1*[0:100] ;
y1 = -x1/2 + 2 ;
x2 = 0.1*[0:100] ;
y2 = -x2/2 + 2 ;

And plot

plot(x1,y1,x2,y2)

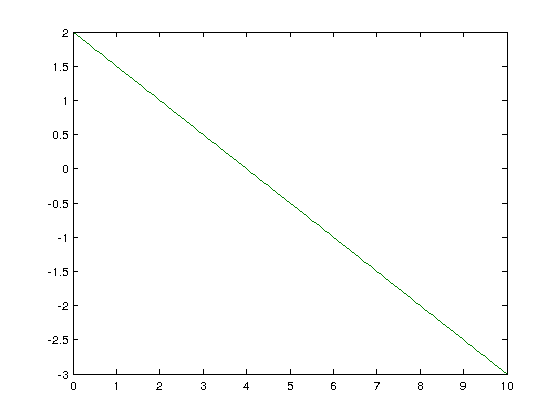
The equation is underdetermined. The determinant should again be zero. Input the equation:

A = [1,2;2,4]
b = [2;4]

and find the determinant

det(A)

ans =
     0

The matrix is not invertible and the \ command does not work

inv(A)
A\b

Warning: Matrix is singular to working precision. 
ans =
   Inf   Inf
   Inf   Inf
Warning: Matrix is singular to working precision. 
ans =
   NaN
   NaN

but we can still solve the system by eliminating one of the equations and moving one of the variable to the right 2*y = -x + 2 = z This can be input as matrices

A = [2]
b = [1]

And solved

A \ b

ans =
    0.5000

Getting y = 0.5000*z = -0.5*x + 1

Linear Systems of Equations

Contents

System 1

System 2

System 3