|
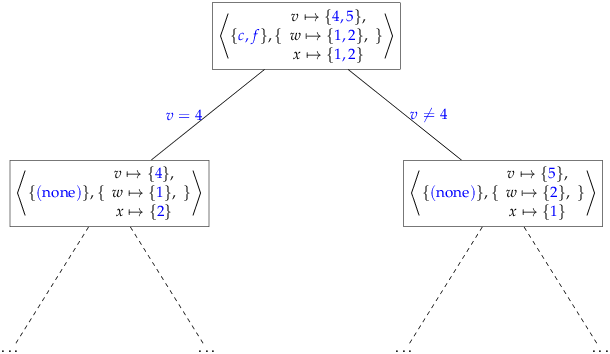
Element(,v,x) (c),
v + x ≤ 7 (d),
w · w ≤ 5 (e),
Distinct({v,w,x}) (f) |
|
Chosen | | Status | Modification | Dependent | Non-subsumed |
FIFO queue Q |
|
prop. | Resulting DE | message | events |
prop.s DepProps | propagators R | of propagators |
|
(none) | v ↦ {}, w ↦
{}, x ↦ {} |
(none) | (none) | (none) |
{} |
[] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |
|
| v ↦ { }, w ↦ { }, x
↦ { } | | | { } |
{ } | [ ] |