DM841 - Discrete Optimization
Exercises, Autumn 2016 [pdf format]

Prepare the following exercises for discussion in class on Thursday 13th October 2016.



Exercise 1 – Modelling

Show that CSP generalizes SAT formulating the following SAT problem as a CSP:

(x ∨ y ∨ ¬ z) ∧ (¬ w ∨ ¬ z) ∧ (w ∨ ¬ y ∨ z)



Solution

Variables: {w(x1), x(x2), y(x3), z(x4)}

Domains: D(x1) = D(x2) = D(x3) = D(x4) = {false, true} = {0,1}

Constraints: C={C(x2,x3,x4) ≡ x2 ∨ x3 ∨ ¬ x4; C(x1,x4)≡ ¬ x1∨ ¬ x4; C(x1,x2,x4) ≡ x1 ∨ ¬ x3 ¬ x4}

In Gecode:

clause(*this, BOT_OR, positives, negatives, 1);

See examples/sat.cpp.

The constraints can be also written as 0–1 linear inequalities of the form aTx ≥ a0. Let ¬ x=x=1−x:

     
x2+x3+x4≥ 1          
1−x1+1−x4≥ 1          
x1+1−x3+x4≥ 1           
     
x2+x3+x4≥ 1          
x1+x4≤ 1          
x1−x3+x4≥ 0           



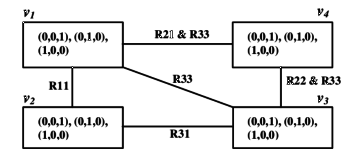
Exercise 2 – Binary CSP

Show how an arbitrary (non-binary) CSP can be polynomially converted into an equivalent binary CSP.



Solution
This can be done in two ways. (see fx [1])

For:

     
C1: x1+x2+x6=1          
C2: x1−x3+x4=1          
C3: x4+x5−x6>0          
C4: x2+x5−x6=0          
           
Figure 1: Dual encoding
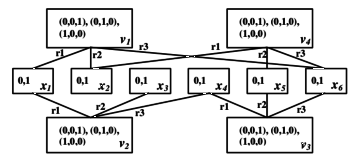
Figure 2: Hidden variables encoding



Exercise 3 – Local Consistency

Are the two following CSPs arc consistent:



Exercise 4 – Local Consistency

Consider the n-queens problem with n≥ 3 and its formulation as a binary CSP that uses the least variables (that is, n variables that indicate the position of the queens, say, on the columns). Is the initial status of this CSP problem arc consistent? If not, enforce arc consistency.



Solution
the binary CSP that models the n-queens problem is

Variables: x1,…,xn with domain [1,…,n] whre xi represents the row position of the queen placed in the ith column.

It is arc consistent. Formally we need to analyse each constraint separately. Consider for instance the constraint xi−xj≠ i−j with 1≤ i<j≤ n and take a∈ [1..n].Then there exists b∈ [1..n] such that a−b≠ i−j: just take b∈ [1..n] that is different from a−i+j.

What about the non-binary formulation?



Exercise 5 – Domain-based tightenings

Given two CSP P and P′, we write P′ ≼ P iff any instantiation I on Y ⊆ X P locally inconsistent in P is locally inconsistent in P′ as well.

Consider the following CSP: P=⟨ X={x,y}, DE≡{D(x)={1,2,3},D(y)={1,2,3}}, C⟩. Construct two domain tightenings P1 and P2 of P (a domain tightening is P′ such that X P′=X P, DE′ ⊆ DE, C P′= C P) for which the relation ≼ defined above is in fact a partial order. (Assume C admits any combination of values as valid.)



Solution
A domain-tightening always gives a partial ordering since it is isomorphic with the partial order ⊆ on DE.

For example:

     
 P1=⟨ X={x,y},  DE≡{D(x)={1,2},D(y)={2,3}}          
 P2=⟨ X={x,y},  DE≡{D(x)={2},D(y)={2,3}}           

Note that domain tightening is a well founded operation, that is, it has a last element (fixed point) because finitely many variables and finitely many values.



Exercise 6 – Propagation on paper

Consider an initial domain expression {x ∈ {0, 1, 2, 3}, y ∈ {0, 1, 2, 3}} and two constraints x < y and y < x. Apply the propagation algorithm Revise2001 from the lecture using pen and paper.



Solution

Not normalized. If we normalize it we discover the problem is inconsitent.

However to apply the Revise2001 we proceed by calculating

Last[x,v,y]

ie, the smallest support for (x,v) on y...

Note that bound arc conssitency could be enforced faster for > with the rules:

     
D(x)← {n ∈ D(x) | n<max[ D(y)]}          
D(y)← {n ∈ D(y) | n>min[ D(x)]}           



Exercise 7 – Directed Arc Consistency

A form of weaker arc consistency is directed arc consistency, which enforces consistency only in one direction. Decide if the following CSP ⟨ x ∈ [2..10], y∈ [3..7], x<y⟩ is directed arc consistent in the case of linear ordering y ≺ x and in the case x ≺ y.



Exercise 8 – Crossword puzzle

Is the initial status of the CSP formulation of the crossword puzzle saw in class arc consistent? If not enforce arc consistency.



Solution

Consider the crossword grid of the figure and suppose we are to fill it with the words taken from the following list:

Variables: x1, …, x8

Domains: X(x1)=D(X2) = {HOSES,LASER,SAILS,SHEET,STEER} etc.

Constraints: a constraint for each crossing. For positions 1 and 2:

     
C1,2 := {(HOSES, SAILS), (HOSES, SHEET),         
 (HOSES, STEER), (LASER, SAILS),         
 (LASER, SHEET), (LASER, STEER)} .          

It is not arc consistent: no word in D(x2) begins with letter I, so for the values SAILS for the first variable no value for the second vairable exists such that the resulting pair satisfies the considered constraint.

Apply AC to the constraint network. See figure:

References

[1]
Roman Barták. Theory and practice of constraint propagation. In In Proceedings of the 3rd Workshop on Constraint Programming in Decision and Control, pages 7–14, 2001.