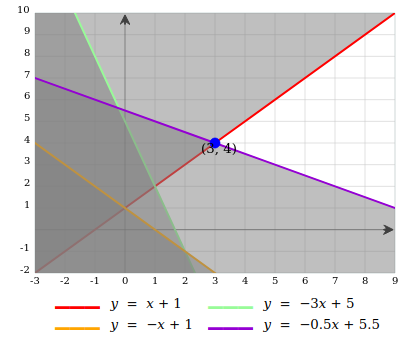
Write an extended formulation with extreme points and extreme rays for the polyhedron
$$ \begin{align*} −x_1 +x_2 &\leq 1\\ 3x_1 +x_2 &\geq 5 \\ x_1 +x_2 &\geq 1\\ x_1 +2x_2 &\leq 11. \end{align*} $$
|--------+--------+--------+--------+--------+--------+--------+--------+
| x1 | x2 | x3 | x4 | x5 | x6 | -z | b |
|--------+--------+--------+--------+--------+--------+--------+--------+
| -1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| -3 | -1 | 0 | 1 | 0 | 0 | 0 | -5 |
| -1 | -1 | 0 | 0 | 1 | 0 | 0 | -1 |
| -1 | -2 | 0 | 0 | 0 | 1 | 0 | -11 |
|--------+--------+--------+--------+--------+--------+--------+--------+
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
|--------+--------+--------+--------+--------+--------+--------+--------+
DUAL SIMPLEX
pivot column: 2
pivot row: 4
pivot: -2
-2
|--------+--------+--------+--------+--------+--------+--------+--------+
| x1 | x2 | x3 | x4 | x5 | x6 | -z | b |
|--------+--------+--------+--------+--------+--------+--------+--------+
| -3/2 | 0 | 1 | 0 | 0 | 1/2 | 0 | -9/2 |
| -5/2 | 0 | 0 | 1 | 0 | -1/2 | 0 | 1/2 |
| -1/2 | 0 | 0 | 0 | 1 | -1/2 | 0 | 9/2 |
| 1/2 | 1 | 0 | 0 | 0 | -1/2 | 0 | 11/2 |
|--------+--------+--------+--------+--------+--------+--------+--------+
| 1/2 | 0 | 0 | 0 | 0 | 1/2 | 1 | -11/2 |
|--------+--------+--------+--------+--------+--------+--------+--------+
pivot column: 1
pivot row: 1
pivot: -3/2
-3/2
|--------+--------+--------+--------+--------+--------+--------+--------+
| x1 | x2 | x3 | x4 | x5 | x6 | -z | b |
|--------+--------+--------+--------+--------+--------+--------+--------+
| 1 | 0 | -2/3 | 0 | 0 | -1/3 | 0 | 3 |
| 0 | 0 | -5/3 | 1 | 0 | -4/3 | 0 | 8 |
| 0 | 0 | -1/3 | 0 | 1 | -2/3 | 0 | 6 |
| 0 | 1 | 1/3 | 0 | 0 | -1/3 | 0 | 4 |
|--------+--------+--------+--------+--------+--------+--------+--------+
| 0 | 0 | 1/3 | 0 | 0 | 2/3 | 1 | -7 |
|--------+--------+--------+--------+--------+--------+--------+--------+
PRIMAL SIMPLEX
Confirm pivot column: 63
pivot column: 3
pivot row: 4
pivot: 1/3
1/3
|--------+--------+--------+--------+--------+--------+--------+--------+
| x1 | x2 | x3 | x4 | x5 | x6 | -z | b |
|--------+--------+--------+--------+--------+--------+--------+--------+
| 1 | 2 | 0 | 0 | 0 | -1 | 0 | 11 |
| 0 | 5 | 0 | 1 | 0 | -3 | 0 | 28 |
| 0 | 1 | 0 | 0 | 1 | -1 | 0 | 10 |
| 0 | 3 | 1 | 0 | 0 | -1 | 0 | 12 |
|--------+--------+--------+--------+--------+--------+--------+--------+
| 0 | -1 | 0 | 0 | 0 | 1 | 1 | -11 |
|--------+--------+--------+--------+--------+--------+--------+--------+
Confirm pivot column: 6
The two points and rays are:
$$ \begin{array}{ll} x_1-1/3x_6&\leq 3\\ x_2-1/3x_6&\leq 4 \end{array} \qquad \begin{bmatrix} x_1\\x_2 \end{bmatrix} = \begin{bmatrix} 3\\4 \end{bmatrix} + \begin{bmatrix} 1/3\\1/3 \end{bmatrix} t $$and
$$ \begin{array}{ll} x_1-x_6&\leq 11\\ x_2=0 \end{array} \qquad \begin{bmatrix} x_1\\x_2 \end{bmatrix} = \begin{bmatrix} 11\\0 \end{bmatrix} + \begin{bmatrix} 1\\0 \end{bmatrix} t $$Consider the mixed integer program
$$ \begin{align} \max\; &4x_1 +5x_2 +2y_1 −7y_2 +5y_3 \\ &3x_1 +4x_2 +2y_1 −2y_2 +3y_3\leq 10\\ &\vec x\leq 3,\; \vec x\in \mathbb{Z}^2_+,\; \vec y\leq 2,\; \vec y\in \mathbb{R}^3_+. \end{align} $$Solve it using Benders’ algorithm.
After solving it, you are informed that the $y$ variables should also be integer. Without starting again from scratch:
We can rewrite the problem in the same matrix terms as seen in the lecture: $$ \begin{align} \max \;& \vec{c}^T\vec{x}+\vec{h}^T\vec{y}\\ &F\vec{x}+G\vec{y}\leq \vec{d}\\ &\vec{x}\in X \cap \mathbb{Z}^q_+ \; \vec{y}\in \mathbb{R}^p_+ \end{align} $$ which in our case becomes: $$ \begin{align} \max\; &\begin{bmatrix}4& 5\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix} + \begin{bmatrix}2&-7&5\end{bmatrix}\begin{bmatrix}y_1 \\y_2\\y_3\end{bmatrix} \\ &\begin{bmatrix}3&4\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix} +\begin{bmatrix}2&-2&3\end{bmatrix}\begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix}\leq 10\\ &\begin{bmatrix}1&0\\0&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}0&0&0\\0&0&0\end{bmatrix}\begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix}\leq \begin{bmatrix}3\\3\end{bmatrix}\\ &\begin{bmatrix}0&0\\0&0\\0&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix}\leq \begin{bmatrix}2\\2\\2\end{bmatrix}\\ &\vec x\in \mathbb{Z}^2_+,\; \vec y\in \mathbb{R}^3_+. \end{align} $$
We will need to use duality theory in the subproblem so we decide to fix the $x$ variables thus leaving the subproblem a linear programming problem. For a fixed $x=\bar{x}$ we get the Benders subproblem: $$ \begin{align} \max\; & +2y_1 −7y_2 +5y_3\\ &2{y}_1-2{y}_2+3{y}_3\leq 10-3\bar{x}_1 -4\bar{x}_2\\ &\vec y\leq 2,\; \vec y\in \mathbb{R}^3_+. \end{align} $$
Next, in some variables $u_1,u_2,u_3,u_4$ we derive the dual of the subproblem (DSP): $$ \begin{align} \min\; &(10-3\bar{x}_1 -4\bar{x}_2)u_1+2u_2+2u_3+2u_4 \\ &2u_1+u_2\geq 2\\ &-2u_1+u_3\geq -7\\ &3u_1+u_4\geq 5\\ &\vec u\in \mathbb{R}^4_+ \end{align} $$
The Benders reformulation (BR), aka extensive formulation (EF), in the extreme rays $v^r, r \in R$ and extreme points $w^p, p \in P$ of $\vec{u}^TG\leq d$ is: $$ \begin{align} z^*=\max\; &4x_1 +5x_2 + \eta \\ &v^r(10-3x_1-4x_2) \geq 0 &\forall r \in R\\ &w^p(10-3x_1-4x_2) \geq \eta &\forall p \in P\\ &\vec x\leq 3,\; \vec x\in \mathbb{Z}^2_+,\; \eta \in \mathbb{R}^1. \end{align} $$
We start the Benders' algorithm by relaxing the integrality constraint on the $\vec{x}$ variables and removing all feasibility and optimality constraints yeilding a reduced extensive formulation (REF): $$ \begin{align} z^*=\max\; &4x_1 +5x_2 + \eta \\ &\vec x\leq 3,\; \eta \in \mathbb{R}^1. \end{align} $$
The optimal solution of the current (REF) is trivial: $z^*=+\infty$, $\eta^*=+\infty$ and $\vec{x}^*=[3,3]$.
import numpy as np
import gurobipy as gp
c = np.array([4,5])
h = np.array([2,-7,5])
F = np.concatenate((np.array([[3,4]]),np.zeros((3,2))),axis=0)
G = np.concatenate((np.array([[2,-2,3]]),np.eye(3)),axis=0)
d = np.array([10,2,2,2])
x_star=np.array([3,3])
def solve_DSP(d,h,F,G,xstar,silent=False):
# Model
m = gp.Model("DSP")
m.setParam(gp.GRB.Param.InfUnbdInfo, 1)
if silent:
m.setParam(gp.GRB.Param.OutputFlag, 0)
# Create variables
u = m.addMVar(shape=G.shape[0], vtype=gp.GRB.CONTINUOUS, name="u")
# Set objective
m.setObjective(u @ (d-F @ xstar), gp.GRB.MINIMIZE)
# Add constraints
m.addConstr(G.T @ u>= h, name="c")
if not silent:
m.update()
m.display()
# Optimize model
m.optimize()
return m, u
dsp_model, dsp_sol = solve_DSP(d,h,F,G,x_star)
if dsp_model.status == gp.GRB.status.INFEASIBLE:
print("Instance infeaasible")
elif dsp_model.status == gp.GRB.status.OPTIMAL:
print("extreme point:", dsp_sol.X)
elif dsp_model.status == gp.GRB.status.UNBOUNDED:
print("extreme ray:",dsp_sol.UnbdRay)
Set parameter Username
Academic license - for non-commercial use only - expires 2024-02-26
Set parameter InfUnbdInfo to value 1
Minimize
-11.0 u[0] + 2.0 u[1] + 2.0 u[2] + 2.0 u[3]
Subject To
c[0]: 2.0 u[0] + u[1] >= 2
c[1]: -2.0 u[0] + u[2] >= -7
c[2]: 3.0 u[0] + u[3] >= 5
Gurobi Optimizer version 10.0.1 build v10.0.1rc0 (linux64)
CPU model: Intel(R) Core(TM) i7-2600 CPU @ 3.40GHz, instruction set [SSE2|AVX]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 3 rows, 4 columns and 6 nonzeros
Model fingerprint: 0x91a40911
Coefficient statistics:
Matrix range [1e+00, 3e+00]
Objective range [2e+00, 1e+01]
Bounds range [0e+00, 0e+00]
RHS range [2e+00, 7e+00]
Presolve time: 0.01s
Iteration Objective Primal Inf. Dual Inf. Time
0 -1.1000000e+31 1.000000e+30 1.100000e+01 0s
Solved in 2 iterations and 0.01 seconds (0.00 work units)
Unbounded model
extreme ray: [0.5 0. 1. 0. ]
We find a ray and a feasibility constraint that is currently violated in the Benders reformulation: $v^r(d-Fx^*) < 0$
dsp_sol.UnbdRay @ (d-F @ x_star)
-3.5
We need to add the feasibility cut $(u^r)^T(d-Fx)\geq 0$: $$ \begin{bmatrix}0.5&0&1&0\end{bmatrix}\left(\begin{bmatrix}10\\2\\2\\2\end{bmatrix}-\begin{bmatrix}3&4\\0&0\\0&0\\0&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}\right)\geq 0 $$ that is: $$ 3x_1+4x_2\leq 14 $$
def solve_REF(c,d,F,extreme_rays=[], extreme_points=[], silent=False):
# Model
m = gp.Model("DSP")
m.setParam(gp.GRB.Param.DualReductions, 0)
if silent:
m.setParam(gp.GRB.Param.OutputFlag, 0)
# Create variables
x = m.addMVar(shape=F.shape[1], ub=3, vtype=gp.GRB.CONTINUOUS, name="x")
eta = m.addMVar(shape=1, ub=100, vtype=gp.GRB.CONTINUOUS, name="eta")
# Set objective
m.setObjective(c @ x + eta, gp.GRB.MAXIMIZE)
# Add constraints
for ray in extreme_rays:
m.addConstr(ray @ (d - F @ x)>=0, name="feasibility cut")
for point in extreme_points:
m.addConstr(point @ (d - F @ x)>=eta, name="optimality cut")
if not silent:
m.update()
m.display()
# Optimize model
m.optimize()
return m,x,eta
ref_model, ref_sol_x, ref_sol_eta = solve_REF(c,d,F, [dsp_sol.UnbdRay])
Set parameter DualReductions to value 0
Maximize
4.0 x[0] + 5.0 x[1] + eta[0]
Subject To
feasibility cut: -1.5 x[0] + -2.0 x[1] >= -7
Bounds
0 <= x[0] <= 3
0 <= x[1] <= 3
0 <= eta[0] <= 100
Gurobi Optimizer version 10.0.1 build v10.0.1rc0 (linux64)
CPU model: Intel(R) Core(TM) i7-2600 CPU @ 3.40GHz, instruction set [SSE2|AVX]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 1 rows, 3 columns and 2 nonzeros
Model fingerprint: 0x8bff916f
Coefficient statistics:
Matrix range [2e+00, 2e+00]
Objective range [1e+00, 5e+00]
Bounds range [3e+00, 1e+02]
RHS range [7e+00, 7e+00]
Presolve time: 0.01s
Presolved: 1 rows, 3 columns, 2 nonzeros
Iteration Objective Primal Inf. Dual Inf. Time
0 1.1866667e+02 8.333333e-01 0.000000e+00 0s
1 1.1825000e+02 0.000000e+00 0.000000e+00 0s
Solved in 1 iterations and 0.01 seconds (0.00 work units)
Optimal objective 1.182500000e+02
We can now write the overall procedure to solve the linear relaxation of the original problem.
extreme_rays=[]
extreme_points=[]
while True:
# We solve the Restricted Benders reformulation (RBR) or restricted extended formulation:
ref_model, ref_sol_x, ref_sol_eta = solve_REF(c,d,F,extreme_rays, extreme_points,silent=True)
if ref_model.status == gp.GRB.status.INFEASIBLE:
print("Instance infeaasible")
break
elif ref_model.status == gp.GRB.status.UNBOUNDED:
print("Ref unbounded:",ref_sol_x.X,ref_sol_eta.X)
break
elif ref_model.status == gp.GRB.status.OPTIMAL:
print("REF solution",ref_sol_x.X,ref_sol_eta.X)
else:
print('Optimization was stopped with status %d' % m.status)
break
# We solve the Dual Subproblem
dsp_model, dsp_sol = solve_DSP(d,h,F,G,ref_sol_x.X, silent=True)
if dsp_model.status == gp.GRB.status.UNBOUNDED:
print("Found extreme ray:",dsp_sol.UnbdRay)
extreme_rays=extreme_rays+[dsp_sol.UnbdRay]
elif dsp_model.status == gp.GRB.status.OPTIMAL:
print("Found extreme point:", dsp_sol.X)
if dsp_model.objVal < ref_sol_eta.X:
extreme_points=extreme_points+[dsp_sol.X]
elif dsp_model.objVal == ref_sol_eta.X:
print("Problem Solved: ",
f"z={ref_model.objVal}, eta={ref_sol_eta.X},"
f"x={ref_sol_x.X}, y={[c.Pi for c in dsp_model.getConstrs()]}")
break
elif dsp_model.status == gp.GRB.status.INFEASIBLE:
print("DSP Instance infeaasible")
break
Set parameter DualReductions to value 0 REF solution [3. 3.] [100.] Set parameter InfUnbdInfo to value 1 Found extreme ray: [0.5 0. 1. 0. ] Set parameter DualReductions to value 0 REF solution [3. 1.25] [100.] Set parameter InfUnbdInfo to value 1 Found extreme point: [3.5 0. 0. 0. ] Set parameter DualReductions to value 0 REF solution [0. 0.] [35.] Set parameter InfUnbdInfo to value 1 Found extreme point: [0. 2. 0. 5.] Set parameter DualReductions to value 0 REF solution [2. 0.] [14.] Set parameter InfUnbdInfo to value 1 Found extreme point: [1.66666667 0. 0. 0. ] Set parameter DualReductions to value 0 REF solution [0.53333333 0. ] [14.] Set parameter InfUnbdInfo to value 1 Found extreme point: [1. 0. 0. 2.] Set parameter DualReductions to value 0 REF solution [1.33333333 0. ] [10.] Set parameter InfUnbdInfo to value 1 Found extreme point: [1. 0. 0. 2.] Problem Solved: z=15.333333333333334, eta=[10.],x=[1.33333333 0. ], y=[-8.881784197001252e-16, 0.0, 2.0]