DM553 - Computability and Complexity
February
Note 1: February 9 (rescheduled: Feb. 13)
Main points: regular languages closed under regular operations (union, contatenation, star) and some others
1.4.c dfa
Construct DFA for intersection of two simple languages. Construct a DFA for each and combine as described on page 46. \(\Sigma = {a,b}\).
\begin{equation*} \left\{ w | \text{even $\#a$ and one or two $b$} \right\} \end{equation*}Even number of \(a\)’s:
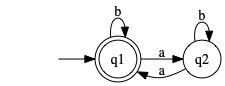
One or two \(b\)’s:
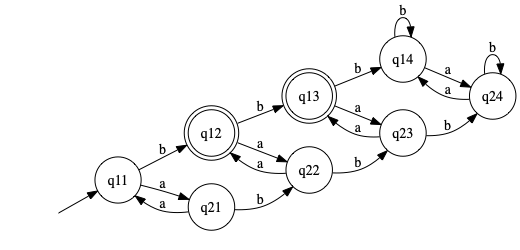
Formal description of combination: Let \(M_1 = (Q_1, \Sigma, \delta_1, q_1, F_1)\) (states, alphabet, transitions, start and accept states) be the first DFA (\(M_2\) similar) . Construct \(M = (Q,\Sigma,\delta,q,F)\) where:
- \(Q = Q_1 \times Q_2\)
- \(\Sigma = \Sigma_1 \cup \Sigma_2\) generally (we assume that \(\Sigma_1 = \Sigma_2\) to avoid dealing with edge cases in transisiont—note that \(\Sigma=\{a,b\}\) in this exercise)
- \(\delta: (Q_1 \times Q_2) \times \Sigma \to Q_1 \times Q_2\) and evaluating it gives: \(\delta((r_1, r_2), a) = (\delta_1(r_1, a), \delta_2(r_2, a))\)
- \(q = q_{11}\)
- \(F = \{q_{ij} \in Q\ \mid\ q_i \in F_1 \wedge q_j \in F_2\}\)
State diagram for combined DFA:
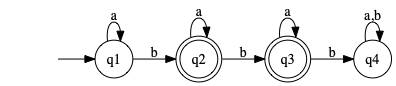
1.5.d dfa
Construct a DFA for a language which is the complement of a very simple language. Approach: construct DFA for the simple language, then “invert” it somehow to get complement.
\begin{equation*} \{w\ \mid\ w \notin a^*b^*\} \end{equation*}State diagram for \(a^*b^*\):
To get complement, use instead \(F' = Q \setminus F\).
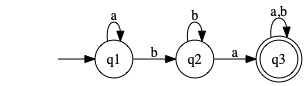
1.6.{c,g,j} dfa
Construct some DFAs. All languages here have \(\Sigma = \{0,1\}\).
- c
Language of strings which contain
0101as a substring. Important note: does not necessarily jump all the way back to start when a “wrong” symbol is read.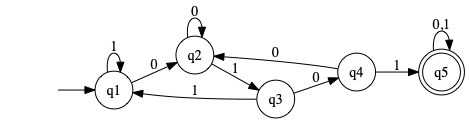
- g
Strings of length at most five:
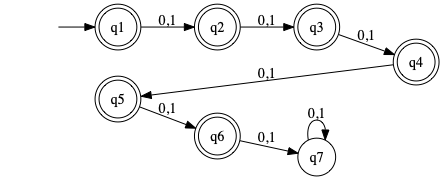
- j
Strings containing at least two 0 and at most one 1. Idea: create two DFAs and combine using intersection-strategy.
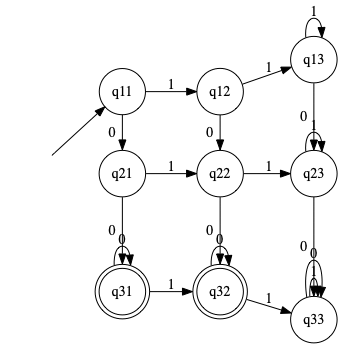
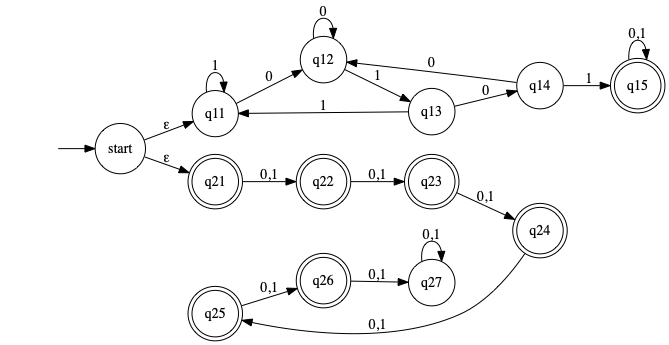
Union of 1.6.c and 1.6.g dfa union
Use thm 1.45 to give state diagrams for NFA for union of the two languages.
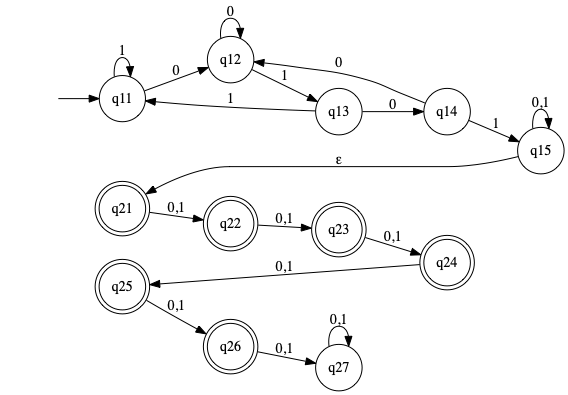
Concatenation of 1.6.c and 1.6.g dfa concat
Use thm 1.47 to give state diagrams for NFA for concatenation of the two languages.
1.31-33 dfa
- 1.31
Perfect shuffle of \(A\) and \(B\) is:
\begin{equation*} \{w\ \mid\ w=a_1b_2 \dots a_kb_k, a_1a_2 \dots a_k \in A, b_1b_2 \dots b_k \in B, a_i, b_i \in \Sigma\} \end{equation*}In short: take strings from each language, intermix their symbols (one at a time). Show: regular languages closed under this operation. Idea: cartesian product of states (like with intersection), but “split them” (double number of states) so the two machines can take turns reading symbols.
- \(Q = \{a,b\} \times Q_1 \times Q_2\)
- \(\Sigma = \Sigma_1 \cup \Sigma_2\)
- \(\delta((a,q_1,q_2),l) = (b,\delta_1(q_1,l),q_2)\) and \(\delta((b,q_1,q_2),l) = (a,q_1, \delta_2(q_2,l))\)
- \(q = (a,q_1,q_2)\)
- \(F = \{(a,q_i,q_j) \in Q\ \mid\ q_i \in F_1 \wedge q_j \in F_2\}\)
- 1.32
Similarly, shuffle of \(A\) and \(B\) is just:
\begin{equation*} \{w\ \mid\ w=a_1b_2 \dots a_kb_k, a_1a_2 \dots a_k \in A, b_1b_2 \dots b_k \in B, a_i, b_i \in \Sigma^*\} \end{equation*}Can reuse construction from 1.31 with added epsilon-transitions. Can simplify, though (note that we don’t need to double the states here).
- 1.33
\(\text{DROP-OUT}(A)\) is all strings from \(A\) with one letter missing.
\begin{equation*} \text{DROP-OUT}(A) = \{xz\ \mid\ xyz \in A,\ x,z \in \Sigma^*,\ x \in \Sigma\} \end{equation*}Show: regular languages closed under this operation (similar to thm. 1.47). Idea: create two copies of DFA recognizing \(A\). Start in the first one which has no accept-states (they are only in the second one). For each transition from some state a to some state b (reading some letter not epsilon), add a “shortcut” transition with ε to state b in second machine (this skips one symbol).
Any path from the starting state in machine one to an accept state in machine two will include exactly one such skipping transition (will be chosen nondeterministically).
Formally, \(\delta'((1,q_i),l) = \{(1, (q_j))\}\) and add \(\delta'((1,q_i),\varepsilon) = \{2, (q_j)\}\) where \(q_j \in \delta(q_i,l)\).
Note 4: February 22
2.4.c,e cfg
Come up with CFG generating languages. \(\Sigma = \{0,1\}\)
c: \(\{w\ \mid\ |w|\text{ is odd}\}\)
- \(S \to 0\)
- \(S \to 1\)
- \(S \to S0S\)
- \(S \to S1S\)
e: \(\{w\ \mid\ w\text{ is a palindrome}\}\)
- \(S \to \varepsilon\)
- \(S \to 0\)
- \(S \to 1\)
- \(S \to 0S0\)
- \(S \to 1S1\)
2.9 cfg cnf ambig
Language:
\begin{equation*} A = \{a^i b^j c^k\ \mid\ i=j \vee j=k, i,j,k \geq 0\} \end{equation*}Come up with CFG. Also: change grammar to Chomsky Normal Form. Note: \(T_c\) will be special variables added with only the rule \(T_c \to c\) for any \(c \in \Sigma\) (used in transformation).
Grammar (seen during lecture I think):
- \(S \to \varepsilon | AX | YC\)
- \(A \to \varepsilon | a | aA\)
- \(C \to \varepsilon | c | cC\)
- \(X \to \varepsilon | bXc\)
- \(Y \to \varepsilon | aYb\)
Adding new starting state, adding derivations with variables removed, removing epsilon-transitions, introducing \(T_l\) where each \(T_l \to l\):
- \(S_0 \to \varepsilon | S\)
- \(S \to AX | YC | A | X | Y | C\)
- \(A \to a | T_aA\)
- \(C \to c | T_cC\)
- \(X \to T_bXT_c\)
- \(Y \to T_aYT_b | T_aT_b\)
Removing / consolidating unit rules (normally would do before, but it’s a lot of writing):
- \(S_0 \to \varepsilon | AX | YC | a | T_aA | T_bXT_c | T_aYT_b | T_aT_b | c | T_cC\)
- \(S \to AX | YC | a | T_aA | T_bXT_c | T_aYT_b | T_aT_b | c | T_cC\)
- \(A \to a | T_aA\)
- \(C \to c | T_cC\)
- \(X \to T_bXT_c\)
- \(Y \to T_aYT_b | T_aT_b\)
Finally, replacing too long derivation rules by chains:
- \(X_1 \to XT_c\)
- \(Y_1 \to XT_b\)
- \(S_0 \to \varepsilon | AX | YC | a | T_aA | T_bX_1 | T_aY_1 | T_aT_b | c | T_cC\)
- \(S \to AX | YC | a | T_aA | T_bX_1 | T_aY_1 | T_aT_b | c | T_cC\)
- \(A \to a | T_aA\)
- \(C \to c | T_cC\)
- \(X \to T_bX_1\)
- \(Y \to T_aY_1 | T_aT_b\)
2.10 dfa
Describe pushdown automaton to recognize \(A\) from 2.9.
Easy part: recognize equal \(a\) and \(b\) by building up, tearing down stack. Similar for equal \(b\) and \(c\). Using nondeterminism, it is trivial to get machine to “choose”. This is basically example 2.16, p. 116.
2.18 cfg ambig
Here is some \(G\):
- \(S \to SS | T\)
- \(T \to aTb | ab\)
Describe \(L(G)\): strings consisting of some number (at least one) of \(a^ib^i\) where \(i \geq 1\) (different for different terms).
\begin{equation*} a^{i_1}b^{i_1} a^{i_2}b^{i_2} \dots a^{i_l}b^{i_l}, \quad l \geq 1, i_k \geq 1 \forall k \in [l] \end{equation*}Show \(G\) is ambiguous by doing the same string in two different leftmost derivations:
- S, SS, TS, abS, abSS, abTS, ababS, ababT, ababab
- S, SS, SSS, TSS, abSS, abTS, ababS, ababT, ababab
Give unambiguous \(H\) s.t. \(L(H)=L(G)\):
- \(S \to ab | HT\)
- \(H \to HT\)
- \(T \to ab | aTb\)
2.30a cfg intersect
\(C\) is context free, \(R\) is regular. Prove that \(C \cap R\) is context free. Idea is again: consider machines \(M_C\) (a PDA) and \(M_R\) (a DFA) recognizing the two languages, combine them to get machine simulating both at the same time. The states will be \(Q_C \times Q_R\) and the transition function (most tricky part) will be something like:
\begin{equation*} \delta((q_c,q_r),a,b) = \left\{ ((q'_c,q'_r),c)\ \mid\ (q'_c, c) \in \delta_C(q_c, a, b) \wedge q'_r \in \delta_R(q_r, a) \right\} \end{equation*}2.31 cfg complement
\(G\):
- \(S \to aSb | bY | Ya\)
- \(Y \to bY | aY | \varepsilon\)
Describe \(L(G)\):
- The first rule for \(S\) gives something like \(a^i w b^i\) where \(w\) is some weird string produced by the other rules and \(|w| \geq 1\)
- \(w\) starts with \(b\) or ends with \(a\)
- \(w\) cannot both start with \(a\) and end with \(b\)
- other than that, anything goes for \(w\)
After thinking for a while (and fooling around with examples): \(L(G)\) has anything in \(\Sigma^*\) as long as it is not \(a^ib^i\) for \(i \geq 0\).
Then, make \(\overline{L(G)}\) based on the description (which by now seems obvious):
- \(S \to aSb | \varepsilon\)
2.32 cfg prefix
Show that \(A\) being context free and \(B\) being regular means \(A/B\) is context free, too.
Consider PDA \(M_A\) recognizing \(A\), DFA \(M_B\) recognizing \(B\). We create a PDA with two parts. The first half if exactly like \(M_A\) and the second half is quite similar to the combination described in 2.30a.
For every state \(q_A\) in the first half, add an epsilon-transition (guessing nondeterministically when \(w\) ends and \(x\) starts) to the state representing \((q_A, Q^0_B)\) in the second half of the machine. Now we can start reading both from here on out.
Issue: want to not actually read anything, just maybe accept. Solution: in second part, make all transitiont read \(\varepsilon\) instead of something (but do transition the same way including stack operations). Then, the machine can nondeterministically find its way to an accept state if such a path exists.
2.33 cfg cnf
\(\Sigma = \{a,b\}\). Give CFG for language where strings have twice as many \(a\) as \(b\). Prove correctness.
- \(S \to \varepsilon\)
- \(S \to aSaSb\)
- \(S \to aSbSa\)
- \(S \to bSaSa\)
- Proof of correctness
Idea: show any string generated satisfies the condition (trivial), show by induction over string length that we can generate all such strings.
Induction base case: \(\varepsilon\) is of course in language. Hypothesis: all \(w\) where \(|w| \leq 3(n-1)\) can be generated (note: all satisfying strings must have length multiple of three). Can we generate \(w\) where \(|w|=3n\) (and \(n \geq 1\))?
Suppose \(w\) starts with \(aa\). Then there must be a way to split \(w\) into \(aaw_1bw_2\) such that \(w_1\) and \(w_2\) are “balanced” (otherwise we can show contradiction). By inductinon hypothesis, we can generate \(w_1\) and \(w_2\). So by using \(S \to aSaSbS\) (and setting some to epsilon), we can get \(aaSbS\) which can then produce \(w\). Similar proof if \(w\) starts with \(ab\).
If instead \(w\) starts with \(b\), we can show that there must be a way to split it into \(bw_1aw_2aw_3\) such that all the \(w_i\) are balanced. Starting after the first letter, scan to the right until there is one \(a\) too many and select this as the first splitting point. This must happen if \(w\) was balanced. Then, after this \(a\) continue and do the same again. Then, apply the hypothesis and see that \(S \to bSaSaS\) means we can generate \(w\).
Note 5: February 28
2.2 cfl
Point of this exercise: point out some things CFLs are not closed under.
- a
Given two languages: \(A=\{a^mb^nc^n\ \mid\ m,n \geq 0\}\) and \(B=\{a^nb^nc^m\ \mid\ m,n \geq 0\}\) and example 2.36 we show that CFLs are not closed under intersection.
- \(A \cap B = \{a^nb^nc^n\ \mid\ n \geq 0\}\)
- Example 2.36 uses the pumping lemma to show that this language is not context free
- The two constituent languages were context free, so the class of CFLs is not closed under intersection
- b
We use DeMorgan’s law in conjunction with part a to show that CFLs are not closed under complement.
- The law in question is \(\overline{A \cup B} = \overline{A} \cap \overline{B}\)
- We know that \(A \cup B\) is context free (see 2.9) and that \(A \cap B\) is not
- If CFLs were closed under complement, we would have \(\overline{A \cup B}\), \(\overline{A}\) and \(\overline{B}\) CFL, too
- Then we could just create the following CFL: \(\overline{\overline{A} \cup \overline{B}} = \overline{\overline{A}} \cap \overline{\overline{B}} = A \cap B\), which we know is not actually a CFL
2.5c,d pda
Do PDAs for some of the languages in 2.4.
- c
Language: \(\{w\ \mid\ |w|\text{ is odd}\}\). This doesn’t even require the stack. Just have two states where one accepts and the other doesn’t. Any character switches state.
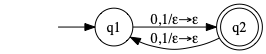
- d
Language: \(\{w\ \mid\ |w|\text{ is odd and middle character is } 0\}\). Idea: use non-determinism to guess when we reach the middle. Build up stack in first half, read a 0, tear down stack after.

2.12 cfg pda
\(G\) from exercise 2.3:
- \(R \to XRX | S\)
- \(S \to aTb | bTa\)
- \(T \to XTX | X | \varepsilon\)
- \(X \to a | b\)
Convert to PDA using procedure from theorem 2.20 (lemma 2.21). TODO: make this look nicer. Graphviz does not handle these multiedges very nicely.
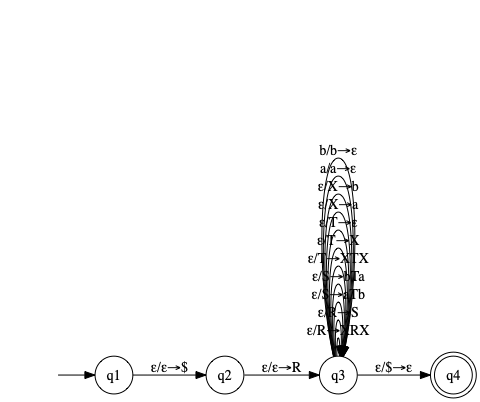
Note that the transitions with multiple things on the right-hand side like \(\varepsilon/S \to aTb\) are actually “implemented” by introducing intermediary states and pushing the individual characters in reverse order one at a time.

2.16 cfl
Show: CFLs closed under regular operations.
- Union union
By grammar: combine two languages union-like by introducing a new start variable which can be changed into either of the start variables of the languages.
By PDA: use non-determinism to decide which machine (for two languages) to use.
- Concatenation concat
By PDA: like with regular languages, we can add one PDA after another by adding epsilon-transitions from accept states of first machine to start states of second. Can empty out the stack between the two for good measure.
- Star star
By grammar: introduce some new \(S_0 \to S_0 S | \varepsilon\).
By PDA: make start accept, add epsilon-transitions from accept to start (maybe empty the stack first).
2.42 cfg pump
Using pumping lemma, show that some languages are not context free. Recall that the pumping lemma for context-free languages says, that there is a length \(p\) for a language \(A\) such that a string \(s\) of length at least \(p\) can be split into \(s=uvxyz\) such that:
- \(\forall i \geq 0: uv^ixy^iz \in A\)
- \(|vy| > 0\)
- \(|vxy| \leq p\)
- a
\begin{equation*} \left\{ 0^n1^n0^n1^n\ \mid\ n \geq 0 \right\} \end{equation*}Consider the string \(0^p1^p0^p1^p\). Observe that if any of \(vy\) “straddle” two different symbols (substring contains both 0 and 1), pumping will immediately mess up the string for \(i > 1\). Considering all other possible combinations of \(\varepsilon\), 0 and 1 for the two strings (but not \(\varepsilon\) for both at the same time), we see that we cannot pump and maintain balance—can at most keep two of the four “parts” in sync.
- b
\begin{equation*} \left\{ 0^n \# 0^{2n} \# 0^{3n}\ \mid\ n \geq 0 \right\} \end{equation*}Consider the string \(0^p\#0^{2p}\#0^{3p}\). Obviously, neither of \(vy\) can contain \(\#\). This means that they can “cover” at most the first and second, first and third or second and third parts, always leaving one behind when pumping.
- c
\begin{equation*} \left\{ w \# t\ \mid\ \text{$w$ is a substring of $t$},\ w,t \in \{a,b\}^* \right\} \end{equation*}Consider \(a^pb^pa^p \# a^pb^pa^p\). Obviously, \(vy\) cannot be contained in \(w\) part only, because pumping would then make this part not a substring. If \(vxy\) were to straddle the \(\#\) and have \(|v|>0\), then \(v\) could only contain some \(a\) in the suffix of \(w\) and \(y\) could only contain some \(a\) in the prefix of \(t\), so pumping would again violate substring condition. Therefore, \(v\) and/or \(y\) must be in \(t\). Note that pumping any \(a\) in \(t\) for \(i \geq 0\) is fine—but for \(i=0\), \(w\) suddenly is not a substring and as \(|vy|>0\), this cannot be avoided.
- d
\begin{equation*} \left\{ t_1 \# t_2 \# \dots \# t_k\ \mid\ k \geq 2, t_i \in \{a,b\}^*, \exists i \neq j: t_i = t_j \right\} \end{equation*}Consider \(a^pb^p\#a^pb^p\). Note that \(\#\) cannot be in \(vy\) as \(i=0\) would then mean that there is no \(\#\) at all. Pumping either side exclusively would obviously make them unequal, so assume \(vxy\) straddles the \(\#\). Due to \(|vxy| \leq p\), \(v\) can only contain \(b\)’s and \(y\) can only contain \(a\)’s, so any pumping \(i \neq 1\) will make the two strings unequal.
March
Note 6: March 7
3.1d tm
Consider TM \(M_2\) that will decide the language \(A = \left\{ 0^{2^n}\ \mid\ n \geq 0 \right\}\):
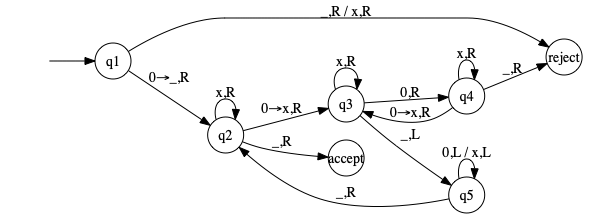
Note slight notation difference relative to book: they use \(0 \to R\) to mean “read \(0\), write \(0\) again and go right” whereas I just use \(\to\) for writing (comma separates read/write and movement).
The sequence of configurations that it enters when started on input string 000000 is:
(q1)000000____(q2)00000____x(q3)0000____x0(q4)000____x0x(q3)00____x0x0(q4)0____x0x0x(q3)____x0x0(q5)x____x0x(q5)0x____x0(q5)x0x____x(q5)0x0x____(q5)x0x0x___(q5)_x0x0x____(q2)x0x0x____x(q2)0x0x____xx(q3)x0x____xxx(q3)0x____xxx0(q4)x____xxx0x(q4)____xxx0x_(reject)__
3.5 tm
Understand the formal definition of a Turing machine and answer:
- Can a TM write the blank symbol on the tape?
- Yes, no problem
- In fact, definition 3.3 mentions that the blank symbol is always in the tape alphabet (from which the transition function can choose freely)
- Can the tape alphabet and the input alphabet be the same?
- No, the blank symbol is never in the input alphabet, but always in the tape alphabet
- Can the head ever be in the same location in two successive steps?
- Technically yes if it tries moving left of the left end of the tape (nothing happens)
- In any other location, can simulate standing still using extra state
- Can the machine contain just one state?
- No according to definition 3.3 since it explicitly requires two distinct states for accept and reject
3.7 tm
We are given a lacking description of a TM \(M_{\text{bad}}\): given input which is a polynomial over variables \(x_1, x_2, \dots, x_k\):
- Try all combinations of assigning integers to \(x_1, \dots, x_k\)
- Evaluate the polynomial on each
- If any setting evaluates to 0, accept—otherwise, reject
Issue: there are infinitely many assignments to try. The third statement is thus nonsensical as the machine can never come to the conclusion that no assignment works (will never reject). Follow-up: is this machine recognizing solutions instead?
3.8b tm recog
Describe TM to recognize language of twice as many 0s as 1s. State diagram omitted for now (hand-drawn). Plan:
- If empty, go to success
- Scan right and cross out two 0s
- May go to fail if end encountered
- Go all the way to the left
- Note: have to indicate start
- Scan right and cross out one 1
- May go to fail
- Go all the way to the left
- Scan to see if there are only xs now
- Could maybe be combined
- Go left
- Go to 2.
3.9 tm decide
On decidability: we consider the language of just one string. 0 means “we will never find life on
Mars” while 1 means “we will find life on Mars some day”. Is this decidable or no? Since in
either case, the language consists of one string which is easy to decide (finite). We just don’t
know which language to decide.
3.16abde tm decide
Show that Turing-decidable languages are closed under some operations
- a: union union
Idea: take two machines, \(M_1\) and \(M_2\) deciding any two Turing-decidable languages. Make one machine \(M\) to emulate both on any given input string. Could do as follows:
- Save a copy of input somewhere (multitape)
- Run \(M_1\)
- If it accepts, accept
- Reset the tape using copy
- Run \(M_2\)
- If it accepts, accept
- Both machines have rejected, so reject
Note: could also use non-determinism.
- b: concatenation concat
Can use non-determinism to split input string into two parts. Run \(M_1\) on first part, \(M_2\) on second part. Accept if both do so, reject if either rejects.
- d: complement complement
Take TM deciding language. Swap accept and reject states. Consider: could we do this for recognizable languages? (no)
- e: intersection intersect
Idea: take two machines, \(M_1\) and \(M_2\) deciding two languages. Make one machine \(M\) to emulate both on any given input string. If both machines accept, accept.
- Save a copy of input somewhere (multitape)
- Run \(M_1\)
- If it rejects, reject
- Reset the tape using copy
- Run \(M_2\)
- If it rejects, reject
- Both machines have accepted, so accept
3.15abd tm recog
Show that Turing-recognizable languages are closed under some operations Main point: difference compared to the decidability-versions due to looping. This is mostly relevant for complement (recognizable not closed under complement) and union (alter proof slightly).
- a: union union
Idea: take two machines, \(M_1\) and \(M_2\) recognizing any two Turing-recognizable languages. Make one machine \(M\) to emulate both on any given input string. Each machine does one step at a time (interleaving necessary). If any of the two machines accepts, accept. Consider: why not run \(M_1\) first, then \(M_2\)?
- b: concatenation concat
Use same approach as b: concatenation. If the first machine starts looping, this particular “branch” of the non-determinism was not supposed to accept anyway.
- d: intersection intersect
Use same approach as e: intersection for decidable. Note that looping is not an issue—if one machine never accepts, the string is not in the intersection anyway.
Note 7: March 8
3.6 tm recog
Discussing theorem 3.21 which says: language Turing-recognizable iff some enumerator enumerates it. Consider wrong simplification of proof one way (given TM, construct enumerator printing its language). \(s_1, s_2, \dots\) are all strings of \(\Sigma^*\)
- For \(i = 1,2,\dots\)
- Run \(M\) on \(s_i\) (original proof: run \(i\) steps on each of \(s_1, s_2, \dots, s_i\))
- If accept, print \(s_i\)
Problem: we don’t know that \(M\) will necessarily halt (only a recognizer).
3.13 tm decide
Show: language decidable iff there is an enumerator enumerating it in standard string order. Main point: consider when / why decidability is important here.
Decidable if enumerable (in order): inspired by theorem 3.21, let the enumerator print out in order. For each string, compare it to original input string. Accept if equal. Due to standard string order, we can tell if the strings output by the enumerator are suddenly “past” the input string. In this case, reject.
Enumerable (in order) if decidable: just like original proof. Enumerate all strings of \(\Sigma^*\) in order, run machine on each and print if accept.
3.17 tm
Write-once TM: can only change symbol on each square of tape at most once. Show: can do the same as a normal Turing machine can.
Hint: start out by considering write-twice TM. Idea: every time we would like to write to a cell for the second time, mark it instead. Then add some delimiter to the end of current tape contents, copy everything up to the mark, then the new symbol and finally the rest of the old contents. This way, we can end up copying the entire contents per step—but it works.
Now for the write-once version, we need to implement the marking without writing twice. We can do
this by using two squares per element instead of one such that each copied symbol a is copied into
_a and to mark it, write the mark on the space. Have to adapt the machine of course such that it
skips past these spaces when reading (extra states in all transitions).
One thing to note for both: consider how the copying works—will probably need to mark the part that has already been copied.
3.18 tm
TM with doubly infinite tape: tape has no left endpoint. To prove: these recognize the class of Turing-recognizable languages.
Suppose we have regular TM recognizing language. Then we create a doubly infinite one where we initially mark the square left of the input by \(\#\). All states get self-loop with \(\#,R\). We can now simulate the regular TM using a doubly-infinite one.
Note that by shifting input arbitrarily to the right (as needed), ordinary TM can emulate doubly-infinite TM. Put some marker on the left-most end of the tape and if we ever want to move further left, shifte everything to the right first.
Alternative suggestions:
- Use multi-tape TM where tape 1 is starting point and everything to the right while tape 2 is
everything to the left of start in reverse order
- Have to make some copy of the states with movement reversed on tape 2
- Have to detect when to switch between the two
- Considering how to implement multi-tape, this is probably similar to above approach
- Make clever mapping such that every odd-numbered \(n\) cell is \((n-1)/2\) on infinite tape while every even-numbered cell except the first one (need marker probably) is distance \((n-2)/2\) to the left of start.
3.20 tm dfa
TM with stay put instead of left: can go right or not move. Never goes to the left again. Show: not equivalent to normal TM, consider what can be recognized. Intuition: can recognize regular languages (have only states and no “memory” as it cannot move backward).
To show that it can only recognize regular, consider how to create an NFA from a stay-put TM (staying put is epsilon). Some care has to be taken if the TM stays while rewriting and changing states (note that doing so does not give it any useful “memory” and we can simulate this using extra NFA states).
4.2 tm dfa regex equiv
Consider problem of showing whether a DFA and a regular expression are equivalent. As a language: all strings which encode first a DFA and secondly a regular expression such that both are equivalent. To determine language, we need to test if the DFA is equivalent to the regex. Recall:
- Can make DFA from regex
- Regular languages closed under intersection, complement (so can subtract)
- \(A=B \iff A \setminus B = B \setminus A = \emptyset\)
- We can decide if a given DFA will accept any string
This one is easy if you know theorem 4.4. Very easy if you know theorem 4.5.
4.4 tm decide cfg
Show: language of CFGs which generate the empty string is decidable.
\begin{equation*} A_{\varepsilon\text{CFG}} = \left\{ \langle G \rangle\ \mid\ G \text{ is a CFG generating } \varepsilon \right\} \end{equation*}In the input, we will have the set of variables. Variable is nullable if it can be rewritten to epsilon or a sequence of nullable variables. Can iterate over all variables and transitions, marking nullable. If starting variable becomes nullable, epsilon can be generated. If not and no changes are found (finite number of variables, rules), epsilon cannot be generated.
Short version: convert to Chomsky normal form (this does the whole nullability thing as a part of it) and check whether or not the starting variable can be rewritten to epsilon.
4.7 basic count
Show: uncountable. Basically, this is an example illustrated nicely on Wikipedia. Given any enumeration of these infinite strings, choose a string which in position \(i\) differs for \(s_i\) at this position (swap 0 and 1 in this case). By construction, this string is not in the enumeration.
4.8 basic count
Show: countable. Just apply diagonal argument (not the negative version) twice. Or remember from discrete math that cartesian product of a finite sequence (here, 3) of countable sets is countable.
Note 8: March 14
4.5 tm recog
Show: \(\overline{E_{\text{TM}}}\) is Turing-recognizable. Once again, consider all strings over \(\Sigma^*\): \(s_1, s_2, \dots\). We make a TM that, given \(\langle M \rangle\) as input will:
- for \(i = 1, 2, \dots\)
- emulate \(M\) on \(s_1, s_2, \dots, s_i\) for \(i\) steps
- if any of those emulations end in accept, then accept (the corresponding \(s_k\) proves that the language of \(M\) is not empty)
4.11 cfg decide
Variable \(A\) in CFG \(G\) usable if it appears in derivation of some string \(w \in L(G)\). Problem: given \(G\) and \(A\), check if \(A\) is usable. Formulate as language, show it is decidable.
Language formulation omitted here. To decide:
- Variable must be reachable
- \(S\) is reachable
- If \(A\) is reachable and \(A \to s_1 B s_2\), then \(B\) is reachable
- Variable must derive something terminal (it must be generating)
- All variables deriving terminals are generating
- If \(A \to BCD\) and \(BCD\) are all generating, \(A\) is generating
Both the sets (reachable and generating variables) can be computed by iterating over grammar a finite number of times. \(A\) must be in intersection.
4.13 cfg decide
Show: it is decidable.
First: convert to Chomsky normal form.
In case we are to check if infinite language: then there will, for long enough strings, be some repetition. This comes from cyclic behavior in expansions. Check if any variable can derive itself (potentially via some intermediaries)—this can be done using a finite number of cycle-detection schemes.
In case it is some finite \(k\), we can first make sure the language is actually finite. In addition, the longest string we can achieve without has bounded length (refer to pumping lemma for rough upper bound). As such length is finite, we can enumerate and test all such strings (thm. 4.7 says that \(A_{\text{CFG}}\) is decidable). Can potentially lower the number of derivations to try, but this is not important.
4.16 dfa decide
From now on: in definitions, I probably omit stuff like “\(M\) is a DFA” because it’s usually implied (you should always write it still).
\begin{equation*} PAL_{\text{DFA}} = \left\{ \langle M \rangle\ \mid\ M \text{ accepts some palindrome} \right\} \end{equation*}Show: it is decidable (hint is to use some theorems about CFLs).
- We know that we can come up with a CFG generating all palindromes.
- We can also intersect CFL with RL to get CFL
- Finally, \(E_{\text{CFG}}\) is decidable
4.21 regex cfg decide
Show:
- PREFIX-FREE(REX) is decidable (given regular expression, decide if its language is prefix free)
- How the same approach does not work to decide PREFIX-FREE(CFG)
First part, DFA approach: convert regex to DFA. For one accepted string to be a prefix of another, the corresponding run through the machine (must be deterministic for this argument) goes from start to some accept to some (maybe even the same) accept again. So do some graph traversal:
- Which accept states are reachable from start?
- For each of these, can any accept state be reached?
If yes for any in the second case, then the language is not prefix-free.
Set theory (theorem gymnastics) approach: \(\Sigma^+\) is regular, so \(L(REX) \cap \Sigma^+\) is regular. It should be empty if and only if \(L(REX)\) is prefix free and \(E_{\text{DFA}}\) is decidable.
Second part, PDA attempt at proof does not really work as traversing the digraph representation does not really cover the language properly. Not all CFGs even have a deterministic PDA.
Set theory attempt fails just because CFLs are not closed under intersection.
4.28
Show that the following is decidable:
\begin{equation*} \left\{ \langle G \rangle\ \mid\ 1^* \cap L(G) \neq \emptyset \right\} \end{equation*}- We know from 2.30a that intersecting a context free language with a regular language gives a context free language
- \(1^*\) is regular, so \(1^* \cap L(G)\) is context free
- We know from thm. 4.8 that \(E_{\text{CFG}}\) is decidable
4.32 dfa decide
Show: can decide whether a given DFA generates an infinite language.
Digraph cycle idea: to generate infinitely many strings, there must be some cycle and from the cycle, it must be possible to reach an accept state.
Language intersection idea: machine having \(n\) states can only accept strings of length \(\leq n-1\) without having to resort to cycles (consider proof of pumping lemma).
- We can create DFA of all \(w \in \Sigma^*\) where \(|w| \geq n\)
- We can intersect it with input DFA
- We can check if resulting language is empty
- If no, original DFA generates strings long enough that language must be infinite
- If yes, original DFA had finite language
Brute force version: check all strings of length \(n \leq k < 2n\) (same purpose as intersection).
Show undecidability of TM halt on epsilon skipped tm undecidable
Suppose we can decide this language using some \(M_{\varepsilon}\). Then, create a TM taking \(\langle M,w \rangle\) as input (encoded machine and some string)
- Create a machine \(M_w\) which, given empty input writes \(w\) on the tape, goes all the way to the
left and then acts like \(M\)
- Just a matter of prepending some finite states to \(M\)
- Run \(M_{\varepsilon}\) with \(M_w\) as input
- Accept if accept
- Reject if reject
This machine would then decide the halting problem. This is a contradiction.
Note 9: March 21
We discuss computable functions. They are of the form \(f: \Sigma^* \to \Sigma^*\) and require that there is some turing machine \(M\) which for any input \(w\) halts with \(f(w)\) on its tape. Definition 5.20 of mapping reducibility \(A \leq_m B\) is: there is a computable function \(f\) such that:
\begin{equation*} w \in A \iff f(w) \in B \end{equation*}5.3 pcp
Post Correspondence Problem, find match in:
\begin{equation*} \left\{ \begin{bmatrix}ab\\abab\end{bmatrix} \begin{bmatrix}b\\a\end{bmatrix} \begin{bmatrix}aba\\b\end{bmatrix} \begin{bmatrix}aa\\a\end{bmatrix} \right\} \end{equation*}I found (using silly brute force approach):
\begin{equation*} \left\{ \begin{bmatrix}ab\\abab\end{bmatrix} \begin{bmatrix}ab\\abab\end{bmatrix} \begin{bmatrix}aba\\b\end{bmatrix} \begin{bmatrix}b\\a\end{bmatrix} \begin{bmatrix}b\\a\end{bmatrix} \begin{bmatrix}aa\\a\end{bmatrix} \begin{bmatrix}aa\\a\end{bmatrix} \right\} \end{equation*}Or:
ab|ab|aba|b|b|a a|a a ab ab|aba b|b|a|a|a|a
5.4 tm mapred
Does \(A \leq_m B\) for regular \(B\) imply that \(A\) is regular?
No! Prove false using contradiction. Favorite non-regular: \(A = \left\{ a^ib^i\ \mid\ i \geq 0 \right\}\). Choice of \(B\) depends on the computable function we wish to construct.
\(B = \left\{ a \right\}\) is finite and therefore regular. Since \(A_{\text{CFG}}\) is decidable, the following is a computable function (could easily make simple TM):
\begin{equation*} f(w) = \begin{cases} a & w \in A \\ b & \text{otherwise} \end{cases} \end{equation*}We see that \(w \in A \iff f(w)\) by construction, so \(A \leq_m B\). But \(A\) is not regular.
5.5 tm mapred
Show: \(A_{\text{TM}}\) not mapping reducible to \(E_{\text{TM}}\) (no computable function reduces the former to the latter).
Suppose it was mapping reducible via some computable function \(f\). Can use on complements (biimplication in definition);
\begin{equation*} w \in \overline{A} \iff f(w) \in \overline{B} \end{equation*}- We have shown that \(\overline{E_{\text{TM}}}\) is recognizable
- Corollary 4.23 states that \(\overline{A_{\text{TM}}}\) is not
- We get a contradiction via thm. 5.28 (\(A \leq_m B\) and \(B\) recognizable means \(A\) recognizable)
5.6 tm mapred
Was moved from note 8.
Prove: \(\leq_{m}\) is transitive. That is,
\begin{equation*} A \leq_m B \wedge B \leq_m C \implies A \leq_m C \end{equation*}We know there are two functions:
\begin{align*} w \in A & \iff f(w) \in B \\ w \in B & \iff g(w) \in C \end{align*}And we need to find \(h\) (actually, TM computing \(h\)) such that:
\begin{equation*} w \in A \iff h(w) \in C \end{equation*}We construct TM for \(h\) as follows: given some input \(w\):
- run \(M_f\), leaving \(w' = f(w)\) on tape
- run \(M_g\), leaving \(w'' = g(f(w))\) on tape
So \(h = g \circ f\) and by definition of \(f\) and \(g\), we know that \(w \in A \iff w'' \in C\).
5.9 tm pcp cfg undecidable
Show: undecidable. Hint: use Post Correspondence Problem (book shows reduction strategy—not depicted here).
Suppose PCP instance solvable, want to show the constructed CFG is ambiguous. Consider multiset giving same string above and below. Can use this to get derivation sequences in grammar. Same strings generated via \(T\) and \(B\) (\(a_i\) only relevant for other direction).
Suppose CFG is ambiguous. Note that the \(a_i\) are new, unique and always at the end of strings, so any string derived from \(T\) is “unique” in this part of the grammar. To generate the same string via \(B\) (only way to get ambiguity), we have to get some \(b\) strings to match the \(t\) strings—but the \(a\) parts ensure that the \(t\) and \(b\) parts used come from matching pairs in the PCP instance.
5.10 tm recog
Show: \(A\) is Turing-recognizable iff \(A \leq_m A_{\text{TM}}\). Important: recognizable and not decidable.
Suppose \(A\) Turing-recognizable, want to show reducibility. Take machine \(M_A\) recognizing \(A\). The following computible function is trivial: \(f(w) = \langle M_A, w \rangle\).
- If \(w \in A\), then \(f(w) \in A_{\text{TM}}\)
- If \(f(w) \in A_{\text{TM}}\), then \(w \in A\)
Suppose \(A \leq_m A_{\text{TM}}\), want to show \(A\) Turing-recognizable. Take the function \(f\) computed by \(M_f\) where we know:
\begin{equation*} w \in A \iff f(w) \in A_{\text{TM}} \end{equation*}We know \(A_{\text{TM}}\) is recognizable, so will recognize if \(f(w) \in A_{\text{TM}}\) and therefore \(w \in A\).
5.11 tm decidable
Show: \(A\) decidable iff \(A \leq_m 0^* 1^*\).
Suppose \(A\) decidable, show reducible. Because \(A\) is decidable, the following function is computable:
\begin{equation*} f(w) = \begin{cases} \varepsilon & w \in A \\ 10 & w \notin A \end{cases} \end{equation*}Second case just needs to be not in \(0^*1^*\). Observe that by construction, \(f\) is a reduction function.
Suppose reducible, show decidable. Consider reduction function \(f\) which is computable. To decide, given any \(w\), whether \(w \in A\), just:
- Compute \(f(w)\)
- Check if \(f(w) \in 0^*1^*\) (trivial)
- If yes, accept
- If no, reject
5.16 tm
Prove Rice’s theorem. \(P\): nontrivial property of language meaning it contains some but not all TM descriptions. And:
\begin{equation*} L(M_1) = L(M_2) \implies (\langle M_1 \rangle \in P \iff \langle M_2 \rangle \in P) \end{equation*}(membership of \(P\) depends only on language of TM)
Proof is tricky, here is annotated version: assume for contradiction decidable for some \(P\) and use this to decide \(A_{\text{TM}}\). Assume \(M_{\emptyset}\) (where \(L(M_{\emptyset}) = \emptyset\)) is not in \(P\). We can take some \(M_P \in P\) because \(P\) is nontrivial. Now, given some \(\langle M, w \rangle\):
- Create a TM \(M'\) which does the following when given \(x\) as input:
- Simulate \(M\) on \(w\), reject if it rejects
- Note that this may loop
- If always looping or rejecting, \(L(M') = \emptyset\)
- Simulate \(M_P\) on \(x\), accept if it accepts
- Simulate \(M\) on \(w\), reject if it rejects
- Use decider for \(P\) to decide if \(\langle M' \rangle \in P\), accept if it is (reject otherwise)
Suppose the constructed \(\langle M' \rangle \in P\). This means that \(M'\) gets past the part where it simulates \(M\) on \(w\) (if it didn’t the language would be empty as it would reject / loop on any \(x\)) to simulate \(M_P\) on \(x\).
Suppose now that \(\langle M, w \rangle \in A_{\text{TM}}\). This means that \(M'\) gets to simulate \(M_P\) on \(x\) which means that \(\langle M' \rangle 'in P\) by construction (could also do contraposition here).
5.18 tm undecidable
Use Rice’s theorem to prove some languages undecidable.
- a
\begin{equation*} INFINITE_{\text{TM}} = \left\{ \langle M \rangle\ \mid\ |L(M)| = \infty \right\} \end{equation*}Rice’s theorem applies:
- Some TMs have infinite languages, others don’t
- Two machines with the same language will also have same language cardinality, so one is included iff the other is included
- b
\begin{equation*} \left\{ \langle M \rangle\ \mid\ 1011 \in L(M) \right\} \end{equation*}- Some TMs have the language of only
1011(can construct one), others don’t (also easy to construct) - If \(L(M_1) = L(M_2)\), then it is obvious that the property applies to both or none (set equality is transitive)
- Some TMs have the language of only
- c
\begin{equation*} ALL_{\text{TM}} \left\{ \langle M \rangle\ \mid\ L(M) = \Sigma^* \right\} \end{equation*}- Some TMs have the language \(\Sigma^*\) (can construct one), others don’t (strict subset)
- If \(L(M_1) = L(M_2)\), then it is obvious that the property applies to both or none
5.28 tm undecidable
Show problem is undecidable (formulate as language first): does given single-tape TM ever write blank symbol over nonblank for given input string?
\begin{equation*} A = \left\{ \langle M \rangle\ \mid\ \exists x \in \sigma^*: \text{when run on $x$, $M$ writes blank over non-blank symbol} \right\} \end{equation*}Suppose for contradiction this is decided by TM \(M_A\). Then we can decide \(A_{\text{TM}}\): given \(\langle M, w \rangle\),
- Create a TM \(M'\)
- Simulate \(M\) on \(w\)
- Note: we don’t want to this simulation to write blank over non-blank; can avoid this by carefully replacing blank character writes during simulation
- If it accepts, write blank over some non-blank symbol (can write non-blank first to have something to overwrite in case there is nothing)
- Simulate \(M\) on \(w\)
- Simulate \(M_A\) on \(M'\), accept if it accepts (reject otherwise)
April
Note 10: April 11 (originally: March 22)
Now exercises are from “Introduction to Algorithms” (3rd ed.) by default.
34.1-3 encode
Describe how to formally encode a digraph as binary string using:
- Adjacency matrix
- Need \(n \times n\) matrix
- Can give \(n\) in unary via 1s (end with 0)
- Knowing \(n\), we can just list the \(n^2\) entries with 0 or 1
- Adjacency list
- Can again give \(n\) (necessary?)
- For each node:
- Give number of outgoing arcs in unary
- Then give ID for each target in unary
34.1-5 polytime
Show: if an algorithm makes at most constant calls to poly-time subroutines and does poly-time additional work, then the algorithm is poly-time.
\begin{equation*} c \cdot n^{k_1} + n^{k_2} \in O\left( n^{\max\{k_1,k_2\}} \right) \end{equation*}Also: show polynomial number of calls to polynomial-time subroutines may give exponential-time algorithm. Suppose we have some algorithm polynomial in its input:
poly(n):
for i=1 to n
do something uninteresting
Now, we make an algorithm calling it polynomially many times:
notsopoly(n):
m = 1
for i=1 to n
m = m*2
poly(m)
Observe that the final call will have the value \(m=2^n\), so the poly-time algorithm will do work that, for the n of the caller, is exponential.
34.2-3 polytime hamcycle dec opt
Show: if HAM-CYCLE is in P, then we can list vertices of such a cycle in order in poly-time.
HAM-CYCLE only tells us whether a hamiltonian cycle exists in the graph. Problem is to extract (and sort) it. Extracting edges (assuming there is cycle in the first place):
for each edge in the graph: remove the edge call HAM-CYCLE algorithm if there is no cycle any longer, add the edge again
This is polynomial and afterwards, graph only contains edges in the cycle. Do clever sorting to run through them in order.
Prove some details on polynomial rejection polytime
Suppose we have \(L\) and algorithm that accepts any \(x \in L\) in poly-time. Algorithm also rejects any \(x \notin L\) (but in super-polynomial time). Argue: can decide \(L\) in polynomial time.
If we know the specific polynomial bound \(n^k\) (function of input size), we can simply run the algorithm for more than \(n^k\) steps. If it has not accepted, we can safely reject.
34.2-4 np
Prove: NP closed under regular operations. In all situations, we have two languages with each their own verification machines.
Union: Try to verify (maybe concurrently?) using both verification algorithms. If one accepts, accept. Note: The certificate could indicate which of the two languages it applies to.
Intersection: Try to verify using both. If both accept, accept. Note: Could combine two certificates with indication of which part certifies which problem.
Concatenation: Combine two certificates with some marker to indicate where to split input string also. Then run each machine on each part and accept if both do.
Skipping Kleene star.
34.2-8 np sat
\(\phi\) is boolean formula over variables \(x_1, x_2, \dots, x_k\). Has \(\neg\), \(\wedge\), \(\vee\) and \(()\).
The language TAUTOLOGY is the language of all such formulas which are tautologies. Show that TAUTOLOGY is in co-NP.
Suppose we have \(\phi\) which is not a tautology. That means for some assignment of values to variables, \(\phi\) is false. Given this assignment and \(\phi\), it is trivial to verify that \(\phi\) can, indeed, be falsified.
34.3-7 polytime np
See 34.3-6 for definitions. Show: Under poly-time reductions, \(L\) is complete in NP iff \(\overline{L}\) is complete in co-NP. Definition of NP-complete gives most of this:
\begin{equation*} \forall L' \in NP \exists f: x \in L' \iff f(x) \in L \end{equation*}And then we just take complements:
\begin{equation*} \forall L' \in NP \exists f: x \notin L' \iff f(x) \notin L \equiv \forall L' \in NP \exists f: x \in \overline{L'} \iff f(x) \in \overline{L} \end{equation*}Note: this gives exactly the definition of \(L\) being complete in co-NP.
Note 11: Started April 11 (originally April 11)
5.29 in Sipser tm decide
In a TM: a useless state is a state that is never encountered on any input string. Formulate as language and show undecidable.
Reducing from \(A_{\text{TM}}\). Plan: given \(\langle M, w \rangle\), make a TM where accept state is useless iff \(M\) does not accept on \(w\). This \(M'\) should just reject on any \(w' \neq w\). Then, when run on \(w\), we want to make sure that, when rejecting, it uses all states except accept.
We can get it to visit all states except accept by introducing new character on tape, making transitions that form a tour of the states ending in reject.
So, suppose \(M_U\) decides useless state language. Create new \(M'\) which given \(\langle M, w \rangle\) will do:
- Create new \(M''\) based on \(M\) which given \(x\):
- All transitions to reject state are replaced by tour to every non-accept state before rejecting
- If \(x \neq w\), then reject
- Otherwise run as normal on \(x\)
- Now, run \(M_U\) on \(M''\)
- If it accepts, then accept state was useless and so reject
- If it rejects, then all states were useful (including accept), so accept
Think about: why do we not need to do tour before accepting?
Find error in argument polytime encoding
Consider algorithm with input \(n\) which is a natural number
- for \(i = 2\) to \(n-1\)
- if \(i\) divides \(n\), then output \(i\)
- output \(-1\) if no divisors were found
Claims made:
- multiplication (and checking) \(n = ik\) takes \(O(\log^2 n)\)
- can use binary search for such \(i\) in \(O(\log n)\) steps
- would use a total of \(O(\log^3 n)\) per iteration
- would use a total of \(O(n \log^3 n)\) to factorize
- can crack RSA in poly-time of input
Joan: Implicitly, we assume that input number is given as binary number. If \(n\) was the value of the number, it is true that the bit-wise representation would have logarithmic length and that iterating over \(n\) would be linear steps. However, size of input is actually number of bits, so the number represented is exponential in input size—loop itself has exponentially many steps.
Create contradiction in formulas sat
Conside Boolean formula with three literals per clause. Show: can add constant number of clauses (also of three literals each) to get formula guaranteed to be false.
Trivial solution: find three variables \(x,y,z\) and add all eight combinations of negating some of them. Each will be unsatisfied by exactly one assignment to \(x,y,z\), but combined, they will cover all possibilities (so the 8 clauses added will be a contradiction independently of formula).
34.3-6 p polytime
Show: Only \(\emptyset\) and \(\{0,1\}^*\) are not complete in P wrt. poly-time reductions.
Recall: \(L_1 \leq_p L_2\) iff there is poly-time computable \(f: \{0,1\}^* \to \{0,1\}^*\) s.t.:
\begin{equation*} x \in L_1 \iff f(x) \in L_2 \end{equation*}So suppose we have a \(L_2\) which is neither empty nor every possible string. There is some string \(a \in L_2\) and some other \(b \notin L_2\). Take any \(L_1\) from P; the following function is trivially computable in poly-time:
\begin{equation*} f(x) = \begin{cases} a & x \in L_1 \\ b & x \notin L_1 \end{cases} \end{equation*}Remember proof for 5.11 (among others) as the idea is very similar.
This approach obviously does not work for \(\emptyset\) and \(\{0,1\}^*\) because it is not possible to use them to “distinguish”.
Note 12: April 18
34.2-5 np
Show: any language in NP could be decided by algorithm running in \(2^{O\left(n^k\right)}\)
Idea by certificates: by definition of NP, any yes-instance has poly-length certificate which can be checked in poly-time. We can, for any string of length \(O(n^k)\), enumerate all the \(2^{O(n^k)}\) certificates of length \(O(n^k)\) and check for each.
34.2-10 np p
Prove: if NP \(\neq\) co-NP, then P \(\neq\) NP.
Contraposition: Suppose P equals NP. This would mean that, for any problem in NP, we can find a solution in poly-time (decider). Then consider the complement; we can just check if any given instance is in the original language and answer in the negative of the result (P is closed under complement due to argument like Prove some details on polynomial rejection). So then P=NP=co-NP.
34.4-4 np sat
Show: determining if boolean formula is tautology is complete in co-NP. Hint: use exercise 34.3-7 which asks to prove that \(L\) is complete in NP iff \(\overline{L}\) is complete in co-NP.
Let complement of TAUTOLOGY be FALSIFIABLE. Can make poly-time reduction from SAT to FALSIFIABLE, so FALSIFIABLE is complete in NP (negation of formula). Via 34.3-7, we conclude then that TAUTOLOGY is complete in co-NP.
34.4-5 polytime p sat
Show: determining satisfiability of formula in DNF is poly-time solvable.
Only need to satisfy one clause. For each clause, try to assign values to satisfy it—there is only one way to do so. If contradiction, just move along. If any satisfiable clause found, we have satisfying (partial) assignment. Else, no solution exists.
34.4-6 sat dec opt
Suppose: we have poly-time algorithm for SAT. How to find assignment in poly-time?
- start with empty assignment
- for each variable:
- assign to true
- if this makes (modified) formula unsatisfiable, assign to false instead
- assign to true
- afterwards: all variables assigned, this is a satisfying assignment
34.4-7 p sat
Consider 2-CNF-SAT. Show that it is in P. Make efficient algorithm. Use \(x \vee y \equiv \neg x \implies y\) and reduce the problem to efficiently solvable digraph problem.
Digraph version: make \(D=(V,A)\) where \(V\) consists of all variables in pure and negated form. \(A\) is then implications. Observe that \(D\) has size polynomial in the size of the formula.
If there is a cycle containing any variable and its negation, then there cannot be a satisfying assignment; in a cycle, all literals must have the same value.
If we know how to find SCCs: In a strongly connected component, there can be no solution iff any \(x\) and its corresponding \(\neg x\) are in the same SCC (by above argument). After building graph, find all SCCs in \(O(m+n)\) and check if any variables have both nodes in same SCC.
Still polynomial: for each variable, see if there is path to its negation (DFS) and back again. This would be \(\Theta(n(n+m))\). Could use Floyd-Warshall instead to achieve this in \(\Theta(n^3)\).
34.5-1 np complete graph
Show: subgraph-isomorphism problem NP-complete. Do we know about clique or independent set? If yes, then this is easy.
Bonus: Assume you have poly-time algorithm solving subgraph-isomorphism problem. Then: use it to find an isomorphism from first graph to subgraph of second graph.
First, we can remove unnecessary nodes from second graph (remove one at a time, add if it removes all mappings). Secondly, we need to determine a bijection between the two vertex sets remaining.
Silly (yet polynomial) strategy: individualize vertices by adding a unique subgraph outside (maybe just a clique of size \(n+1\)) and connecting to only one node on both sides.
Faster (but to me less obviously correct): remove vertex in second graph one at a time. For each one, find the corresponding vertex in first graph by removing one at a time here.
34.5-2 np complete sat
Show: 0-1-integer-programming problem NP-complete via reduction from 3-CNF-SAT. Let \(A\) have dimensions \(m \times n\) where \(m\) is number of clauses, \(n\) is number of variables. The 0/1-vector \(x\) will have \(n\) entries, each representing a variable (0 for false, 1 for true).
Each row in \(A\) models a clause; it has only 3 non-zero entries which are 1 for negated variables and -1 for regular ones. The corresponding row in \(b\) will have value equal to number of negated variables minus one.
Example: \((\neg x_1 \vee x_2 \vee x_3)\) will in \(A\) appear as \(1\ -1\ -1\). Row with 100 is bad and has sum 1. All others fine and have sum \(\leq 0\).
| x1 | x2 | x3 | sum |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | -1 |
| 0 | 1 | 0 | -1 |
| 0 | 1 | 1 | -2 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | -1 |
Bonus: try reduction from vertex cover. Here, \(A\) can have dimensions \(m \times n\) such that each row represents an edge (has two non-zero entries indicating endpoints). If endpoints are -1 and \(x\) has entries 1 for each selected node, then each entry of \(b\) is just -1.
Problem: resolve the problem that this only gives a vertex cover. What about guaranteeing that it has size something? Idea: add an extra row which counts the number of selected vertices. Row should have all ones. Corresponding entry in \(b\) should be target number of vertices.
Note 13: April 19
34.5-4 polytime
Show: if target value of subset-sum problem is given in unary, problem can be solved in poly-time. Point: target value has now magnitude polynomial in input size. Could use the merge-list exact sum algorithm from the book.
Also: Any pseudopolynomial solution will therefore be actually polynomial. Example: dynamic programming solution which takes time \(O(sn)\) where \(s\) is sum to hit.
34.5-5 np complete
Show: set-partition problem is NP-complete. Trivial part: argue it is in NP.
Reduction from subset sum. Consider instance \((A=\{a_1,a_2,\dots,a_n\}, t \in \mathbb{Z})\) of subset sum. Let \(S = \sum_{i=1}^{n}a_i\). Create then an instance \(A' = A \cup \{S - 2t\}\) of set partition. We now prove this is a valid reduction (given: it is polynomial).
Suppose there exists a subset \(B \subseteq A\) s.t. \(\sum B = t\) (solution to subset sum). Then, \(\sum(A \setminus B) = S-t\) and \(\sum (B \cup \{S - 2t\}) = S-t\), so there exists a satisfying partition.
Suppose there is a satisfying partition. Each must have sum \(S-t\) by construction. One of the parts, \(B'\) will contain \(S-2t\). Removing this element, we see that \(\sum(B' \setminus \{S-2t\}) = t\), so we have subset sum solution.
Reduction found in old notes: choose some \(w > \max\{S,t\}\) and use partition instance \(A \cup \{w-t, w-S+t\}\).
34.5-6 np complete hamcycle
Show: hamiltonian-path problem is NP-complete. Trivial: it is in NP. Reduction from HAM-CYCLE:
- for each edge
- create new graph without this edge
- for the two endpoints, add new nodes with only connections to one of the endpoints
- if there is a HAM-PATH in this graph, there was a HAM-CYCLE using the removed edge in the original graph (and vice versa)
34-2 np complete polytime
Variations on problems involving a bag of stuff to be divided between Bonnie and Clyde. For each, show NP-complete or give poly-time algorithm.
- a
\(n\) coins, only two different kinds. Divide evenly. In P. Can do clever balancing algorithm, but even silly brute force works; suppose \(n_1\) coins have value \(v_1\) and \(n_2\) have \(v_2\). Let the goal (half) be \(t\).
- for \(i=1 \dots n_1\)
- for \(j = 1 \dots n_2\)
- if \(i v_1 + j v_2\) = t$
- return true
- if \(i v_1 + j v_2\) = t$
- for \(j = 1 \dots n_2\)
- return false
Note: polynomial (even with the multiplication stuff) because each element is already listed in input (the operations are polynomial in the representation we are given).
Note also: polynomial for any constant number of different denominations.
- for \(i=1 \dots n_1\)
- b
\(n\) coins, arbitrarily many kinds—but all denominations are powers of two. Can be solved polynomially. Let half of total sum be \(t\) again.
- while \(t > 0\)
- if any remaining coins have value \(v < t\)
- let \(x\) be the biggest of these coins
- \(t \gets t - x\)
- remove \(x\) from bag
- else return false
- if any remaining coins have value \(v < t\)
- return true
Argument to make: biggest power of two not greater than remaining part is in solution (easier to argue in recursive formulation). If it is given to Bonnie and Clyde cannot get enough (smaller) coins in any way, then there was no solution. If Clyde can get at least the same amount in (not greater) coins, then a subset of these have the same value as the big one.
- while \(t > 0\)
- c
\(n\) checks with arbitrary amounts on them. This is obviously the set-partition problem in disguise.
- d
\(n\) checks, but Bonnie and Clyde are okay with an unfair split; difference must be at most 100 dollars. By blowing up values of set-partition by a factor of more than 100, this should be the same. Blowup is polynomial.
Note 14: April 25
34-3 np complete coloring
Note: this was also in note 13 (moved here as it was not covered last time). Graph coloring. An instance is \(G\) and it is minimization problem (minimum number of colors).
- a
Find 2-coloring efficiently if one exists. Just do DFS or BFS and keep alternating between two colors. If a conflict is detected, then there really was no solution anyway (cycle of uneven length is detected).
- b
As decision problem (is there a \(k\)-coloring?): show it is poly-time solvable iff graph coloring (finding minimum number of colors) is. Right-to-left is trivial. Left-to-right: we must use decider for \((G,k)\) instances to find actual coloring.
- for \(i = 0 \dots n\)
- if \(G\) admits an \(i\)-coloring
- return \(i\)
- if \(G\) admits an \(i\)-coloring
- for \(i = 0 \dots n\)
- c
3-COLOR: language of graphs which admit 3-colorings. Show: if NP-complete, then decision problem from b is, too. Simply observe that 3-COLOR is special case \(k=3\) of the decision problem.
- d
Read reduction from 3-CNF-SAT to 3-COLOR and start explaining why it works.
- For each variable, create vertex for true and vertex for negated
- For each clause, 5 vertices are created
- 3 special vertices, true/false/red, are created in addition
- Clause edges follow from widget below
- Literal edges form triangles:
- 3 special vertices are in one
- Each variable \(x\) has \(x\), \(\neg x\) and red as triangle
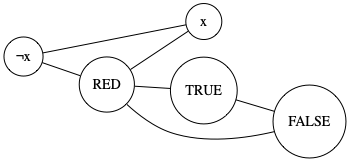
Now argue: any c-coloring on the graph with the literal edges means that each variable has different colors for true and false. This is trivially true by the fact that the variables are connected to their inversion.
Argue: for any truth assignment (consistent), there is a 3-coloring on graph with just literal edges. As neither \(x\) nor \(\neg x\) can be same color as RED (and neither can TRUE nor FALSE), one of them has same color as TRUE, the other has same color as FALSE. Given an assignment, this coloring is easy to realize.
- e
Argue that a widget used in the proof works; it should be 3-colorable if and only if at least one of \(x,y,z\) is colored true (original clause \((x \vee y \vee z)\)).
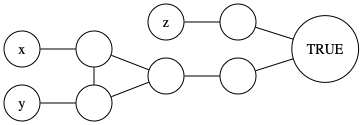
If all three are colored false, then there is no 3-coloring. Check for 1/2/3 colored true that a 3-coloring can be found. Important to keep the literal edges in mind when checking this.
- f
Prove: 3-COLOR is NP-complete. We have the construction for the reduction. It is polynomial in size. Literal edges enforce consistency, clause edges mean that there is coloring iff there is satisfying assignment.
Note that 3-COLOR is trivially in NP (consider how to check a given coloring).
3.10 from notes p141 selection
Show: can find median of five elements using six comparisons in worst case. Start by comparing two pairs of elements. Suppose a<b and c<d. Then, compare the two losers; suppose a<c. We can discard a now.
We have now b (bigger than one element), c (smaller than one, bigger than one), d (bigger than one) and e (uncompared). We compare b with e and have two cases:
- b<e means we have two “chains” a<c<d and a<b<e
- compare and wlog assume c<b (symmetric)
- now a<c<d and a<c<b<e means only d or b can be median; take the smaller one
- compare and wlog assume c<b (symmetric)
- b>e means we have (a,e)<b and a<c<d
- compare e with c, giving two cases
- e<c means (a,e)<b and (a,e)<c<d so only b, c remain as candidates; take smaller one
- e>c means a<c<d and a<c<e<b, leaving d,e as candidates; take smaller one
- compare e with c, giving two cases
Lower bound for list merging lowerbound adversary
Have sorted lists of length \(n\) and \(m\), wish to merge. Prove (tight) lower bound of \(n+m-1\).
Consider final list of length \(n+m\). If only \(n+m-2\) comparisons were used, there must be a pair of consecutive elements which were not compared. Suppose these came from two different lists (can create input so this happens); we can then run the algorithm again where they should be from same list and as the algorithm cannot distinguish, it will be wrong in one case.
Some problems from book by Baase
Determining if bit strings have two zeroes adversary
Adversary forcing n checks or algorithm.
- n=2 obvious adversary: say 0 first (have to check the other)
- n=3 almost obvious adversary
- if 2 is queried, answer 0 (from here, obvious)
- if 1 or 3 is queried, answer 1 and proceed with n=2 strategy
- n=4 has algorithm querying only 3, starting with 2
- if 1, we can ignore 1 and proceed with 3,4 (3 checks in total)
- if 0, query 3
- if 0, done
- if 1, we can ignore 4 and need only check 1 (3 checks in total)
- n=5 has clever adversary; for any query, we give response
- if 1 is queried, answer 0
0____01___reduces to n=30_1__reduces to n=2 and 2 must be queried0__0_can force all to be queried (answer 1)0___101__1reduces to n=20_0_1remaining must be queried (answer 1)0__01ditto
- if 2 is queried, answer 0
_0___10___101__n=2 remaining10_0_both remaining must be queried (answer 1)10__0ditto
_01__already covered (will always set 1 to 1)_0_0_ditto
- if 3 is queried, answer 1
__1__- this reduces to two cases of n=2 where adversary is known
- if 1 is queried, answer 0
One of k smallest lowerbound
- Algorithm
Have \(n\) keys and integer \(1 \leq k \leq n\). Have to find one of the \(k\) smallest keys. Idea: naive linear minimum algorithm on the first \(n-k+1\) elements using \(n-k\) comparisons.
- Lower bound
Suppose we could find it in \(n-k-1\) comparisons. Can then make adversary make us give \(n-k-1\)’st key which is wrong. With \(n-k-1\) comparisons, we know that \(n-(n-k+1)\) subsets of elements have not been compared to each other (think of Hasse diagrams). Therefore, the adversary can choose to say that whichever element we select—even if it is minimum of some subset—is \(k+1\)’th instead of among \(k\) smallest.
Selection in two sorted lists selection lowerbound
L1 and L2 are arrays. Each has \(n\) keys and is sorted. Find the \(k\)’th smallest element.
- Give an algorithm
\(O(\log n)\) by doing alternating divide and conquer / binary search.
- let x be median element (in middle) of L1
- do binary search for x in L2, let i be index of smallest element greater than x
- if \(n/2+i = k\), return x (maybe off by one)
- if \(n/2+i > k\), recurse with L2[:i], L1[:n/2], k
- else recurse with L2[i:], L1[n/2:], k-n/2-i
Can improve to \(O(\log k)\) by noting that we only care about up to first \(k\) elements of each
- Give a lower bound
Information theoretic bound: there would be \(2n\) (or \(2k\)) leaves in decision tree, giving a depth of \(\Omega(\log n)\) (\(\Omega(\log k)\)).
Finding the third largest item algo
Naive way: use maximum finder three times; first two times discarding maximum. This would take \(n-1+n-2+n-3=3n-6\) comparisons.
Could also: maintain top three all the time. Worst case involves swapping each time. Would require \(0+1+2+3(n-3)=3n-6\) comparisons.
Sorting by reversals algo lowerbound
- Algorithm
Suppose we just:
- for i=1 to n
- find minimum of A[i:] with index j
- reverse interval [i,j]
This way we do at most n-1 reversals
- for i=1 to n
- Lower bound
Consider the sequence
1 3 5 7 ... n-1 2 4 6 8 ... n.- For n=4 or above, no number has correct neighbour
- A reversal changes neighbours for at most 4 numbers
- At least \(n/4\) reversals must be performed
- Why can’t we use ordinary lower bound?
Algorithm is not analyzed in decision tree model under comparisons.
May
Note 18: May 17
35.4-4
Look at LP relaxation of integer programming version of vertex cover:
\begin{align*} \min \sum_{v \in V} w(v) x(v) &&\\ x(u) + x(v) & \geq 1 & \forall (u,v) \in E\\ x(v) & \leq 1 & \forall v \in V\\ x(v) & \geq 0 & \forall v \in V \end{align*}Consider a solution satisfying all constraints with some \(x(v) > 1\). Note that \(x\) is positive and so is \(w\), so lowering this value to \(x(v)\) would decrease the total weight sum (solution was not minimal) and it would still be a solution.
35-2
We discuss the problem of maximum clique finding, MAX-CLIQUE. \(G^{(k)} = (V^{(k)}, E^{(k)})\) where \(V^{(k)}\) is all ordered \(k\)-tuples of vertices of \(V\) and an edge is in \(E^{(k)}\) between \((v_1,v_2,\dots,v_k)\) and \((w_1,w_2,\dots,w_k)\) if, for \(i=1 \dots k\), either \(v_i = w_i\) (note tuples can have repeat vertices) or \((v_i,w_i) \in E\).
- a
Show: \(G\) has max-clique of size \(c^{\star}\) iff \(G^{(k)}\) has max-clique of size \(c^{\star}\). Will do this by proving every clique in \(G\) of size \(c\) corresponds to clique of size \(c^{k}\) in \(G^{(k)}\).
Consider a clique \(C\) of size \(c\) in \(G\). In \(G^{(k)}\), the vertices of \(C\) give rise to \(c^k\) ordered tuples, \(C^{(k)}\). As \(C\) is a clique, all pairs of vertices in \(C^{(k)}\) are connected, too, and so it is also a clique.
Consider a set of vertices \(C\) in \(G\) that is not a clique. In \(G^{(k)}\), the vertices of \(C\) consisting of tuples over these vertices will not all be connected and so \(C^{(k)}\) is not a clique.
- b
Show: if we have any constant-factor approximation algorithm for MAX-CLIQUE problem, then we can also create a PTAS for MAX-CLIQUE. If we had approx. ratio \(r\), then we could:
- pick some \(k\)
- create \(G^{(k)}\)
- use the algorithm on this graph to find \(C^{(k)}\)
- find corresponding \(C\)
Now compare max clique size \(c^{\star}\) to this;
\begin{equation*} \left| C^{(k)} \right| = c^k \leq {c^{\star}}^k \leq r c^k \implies \left| C \right| = c \leq c^{\star} \leq r^{-k} c \end{equation*}So as \(r>1\), the interval becomes quite small. We have a PTAS.
35-4
We now look at the maximum matching problem and end up having a polynomial-time approximation algorithm.
- a
First: show that a maximal matching is not necessarily maximum. This is trivial; u-shaped graph with four vertices and three edges has two different maximal matchings, of which only one is maximum.
- b
Polynomial-time algorithm for getting maximal matching:
- \(M \gets \emptyset\)
- for \(e \in E\):
- if \(e\) is not incident to anything in \(M\):
- \(M \gets M \cup \{e\}\)
- if \(e\) is not incident to anything in \(M\):
Consider: how to make the check constant-time s.t. the runtime is \(O(E)\).
- c
Argue: size of maximum matching is lower bound for size of vertex cover.
Main point: the vertices incident to edges in the matching are all disjoint. To cover the edges in the vertex cover setting, each edge in a matching must have one vertex in the cover. Due to disjointness, no vertex in the cover can cover two edges in the matching.
- d
Consider maximal matching \(M\) and let the vertices incident to \(M\) be \(T\). Consider induced subgraph by removing \(T\), \(G-T\). We see that \(G-T\) is independent!
- \(M\) is maximal, so \(\not \exists (u,v) \in E: u \notin T \wedge v \notin T\)
- Therefore, for any \(u\) and \(v\) in \(G-T\), \((u,v) \notin E\)
- e
Argue: there is vertex cover of size \(2|M|\). Just consider previous observation; when \(G-T\) is independent, then \(T\) covers all edges of \(G\). \(|T|=2|M|\).
- f
Now show: have approximation algorithm. Let \(C^{\star}\) be minimum vertex cover. \(M\) is found maximal matching, \(M^{\star}\) is maximum matching.
\begin{equation*} |M| \leq \left| M^{\star} \right| \leq |C^{\star}| \leq 2|M| \end{equation*}
35-5
We look at the parallel machine scheduling problem. Have:
- Jobs \(J_1, \dots, J_n\)
- Processing time \(p_i>0\) for each job \(i\)
- Machines \(M_1, \dots, M_m\)
We define \(C_i\) to be completion time for job \(i\). \(C_{\max}\) is makespan (completion time for last job); this is what we wish to minimize in our job schedule.
- a
Show: lower bound for minimum makespan, \(C_{\max}^{\star} \geq \max\{p_i\ \mid\ i \in \{1,2,\dots,n\}\}\). This is quite trivial (longest job has to go somewhere).
- b
Show: alternative lower bound, \(C_{\max}^{\star} \geq \frac{1}{m} \sum_{i=1}^{n} p_i\).
Intuition: Consider perfectly balanced schedule where every machine has same (average) load. This is clearly the best solution; any rearrangement would make maximum bigger.
If all machines were to run for less than the specified time, then summing the total work they had done would be strictly less than the sum of the job times, which is impossible.
- c
Give an efficient algorithm that will assign jobs to next free machine.
- let \(Q\) be an empty priority queue
- insert \((0, M_j)\) into \(Q\) for \(j=1\) to \(m\) (0 is priority/key)
- for \(i=1\) to \(n\):
- \((t, M) = \text{ExtractMin}(Q)\)
- schedule job \(J_i\) to start on machine M at time \(t\)
- insert \((t+p_i, M)\) into \(Q\)
Can be done in \(O(m + n \log(m))\) with binary heap.
- d
Show: makespan of solution found by algorithm is at most the average (question b) plus longest processing time (question a). This is done by considering how jobs are assigned. Crucial observation: machine to finish last has only one job running after the others have stopped (algorithm would not schedule more jobs to it).
We now have a proof that we have an approximation algorithm (factor is 2). Let \(\max_p\) be longest processing time and \(\text{avg}_p\) be average over machines (from b):
\begin{equation*} \max\left\{\max_p, \text{avg}_p \right\} \leq C_{\max}^{\star} \leq \text{avg}_p + \max_p \leq 2 \max\left\{\max_p, \text{avg}_p \right\} \end{equation*}