Final Assignment

Instructions

To pass DM560 you have to pass the two class tests and a final assignment. In this document you find the requirements for the final assignment.

The final assignment has to be carried out individually.

The submission deadline is:

Monday, January 20, 2020 at 23:59

To pass the assignment, you have to hand in a software project and a written report about it. Everything has to be uploaded as a single zip file in the open SDU Assignment in BlackBoard. The zip file must contain the following:

• report.pdf: this is the written report.

• code: a directory containing all source code of the software project.

Detailed instructions on the two items are given below.

Report

The report must be written in Danish or English and be at the most 3 page long.

Use default line spacing and ensure that the page margins are at least 3cm (in all directions). For the body text use Times New Roman as family and 11pt as font size.

In the first page, you must state the name of the course, your name, your e-mail address, and the date (in which you last edited the document). The report must contain the following sections:

• Structure. Here you explain how you designed your program. Give a brief overview of the classes and how your program works.

• Tests. The results of the tests conducted on your code.

• Advantages. Here you have to explain the nice points of your implementation, i.e., the advantages that come out of your design choices.

• Limitations. Here you have to explain the limitations of your approach and, possibly, how they could be overcome. Did you sacrifice performance for achieving better readability of your code? Or, did you sacrifice readability for improving efficiency? Is there a way to improve? Is there something that does not work as expected? Are there known bugs in your program?

Inspiration points to discuss advantages and limitations:

• Readability
• Speed
• Memory consumption
• Reusability (the code can be reused in different contexts)
• Scalability (scales well with memory usage)
• Reliability (handling of errors/exceptions)

Software

Organize your files in a directory called Topic1. Inside this directory create a directory src/ containing all source files .h and .cpp that you have created for the assignment. Include a Makefile to compile your program.

Hence, the zip file must uncompress as follows:

└── Topic1
    ├── report
    |   └── report.pdf
    └── src
        ├── Makefile
    	├── file.h
        └── file.cpp

The files file.* can have different names and can be as many as you need. However, the structure and organization of your code is also important and is under assessment.

The code must compile and execute without errors on the tests described in the report. The reference environment where the code must work as expected is the IMADA Computer Lab.

Lift Simulator

The goal of the assignment is to design and implement a simple lift control system using C++. (Lifts and flats are UK terms, in the same way that elevators and apartments are North American terms.)

You will model the operation of the hypothetical lift control system of a building, with a fixed number of lifts, a fixed number of floors between which lifts travel, and users. The figure gives an abstract view of what our building looks like.

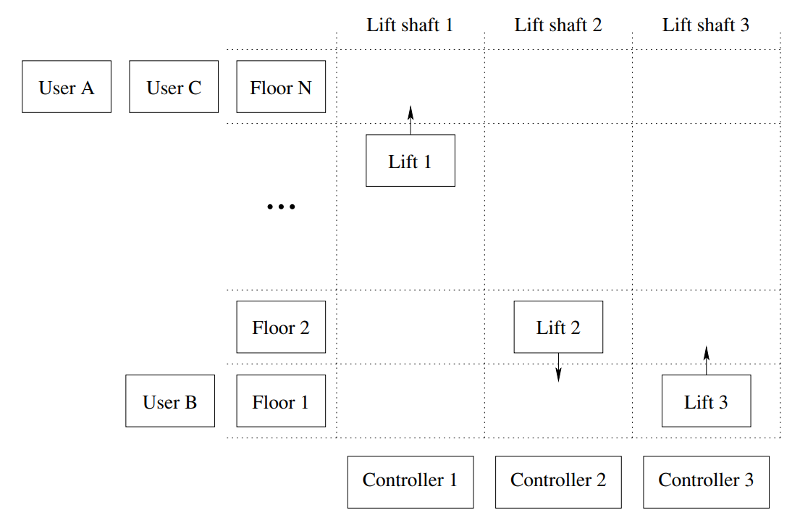
There are floors, lifts, controllers for lift movement, and users that come and go. You will model what happens when a user calls a lift to go to another floor and how the lifts move and you will implement a program to simulate the behaviour of the system in a time span with random users arrivals and users requests.

Task 1

Initially, we will be satisfied with a partial specification of the problem. There are a set of floors and a single lift. Each floor has a call button that users can press. The call button (O, for origin) does not specify an up or down direction. The lift has a series of call buttons (D, for destination) numbered for all destination floors, to tell it to stop at a given floor. The lift has a schedule, which is the list of floors that it will visit in order.

The scheduling algorithm you should use in this first task is called FCFS (first-come, first-served): a new floor is always added at the end of the schedule. This is the same as FIFO scheduling. Both the call O and call D buttons do FCFS. This is not the best scheduling algorithm for lifts, but it has the advantage of simplicity. Later we will see how to improve it. When the lift arrives at a scheduled floor, the doors open and stay open for a fixed time before closing. When moving the lift takes a fixed time to go from one floor to the next.

The lift control system can be designed as a discrete-event simulation with fixed-increment time progression. Time is broken up into small time slices and the system state is updated according to the set of events/activities happening in the time slice.

Hence, we will have four kinds of components, namely floors, lifts, controllers, and timers. All component instances can be designed as user-defined objects. Controllers are used to handle lift motion. Timers handle the real-time aspect of the system by progressing time.

Because of FCFS scheduling, the lift will often move much farther than necessary. If the lift is on its way from one floor to another, then calling an intermediate floor will not cause the lift to stop there. We can avoid these problems by making the scheduler more intelligent. Once we have determined the structure of the whole application, it will become clear how to do this and other improvements.

Implement the system and simulate a scenario with a resonable set of user requests for the real-time duration of one hour. Make the number of arrivals per hour a parameter of the program. Report measures of performance, for example, how much time did the worse case last? How much has been the total waiting time? How much has been the total completion time?

Task 2

The second task asks to add the functionality of having a number of lifts all behaving like in the first task.

The floor randomly choose the lift that will cover the request. That is, if a lift is already at a floor, then calling that floor again may call another lift.

Implement also this system, adding the number of lifts to the list of parameters of the program and report the measures of performance.

Task 3 (optional)

Consider other scheduling algorithms and compare their perfomance with the FCFS scheduling.

Questions and answers

Questions and answers will be published as they are processed at this link.

Implementing a Simulator

In a synchronous simulator we a state refers to the current state of all objects in the simulator at a specific point in time. A tick is a single action in which the current simulator state is updated exactly once with respect to some time step. The simulator loop controls the overall flow of the simulator by executing ticks repeatedly.

Simulator loop

The simulator loop has the following parameters:

• $tps$ the number of ticks performed per second [ticks/s]
• $TAPT$ the simulation time advancement per tick (or time step) [s/tick]

Consider the relation: $tps \cdot TAPT = \rho$

where $\rho \geq 0$ is the simulator time dilation factor.

• If $ρ = 1$, the simulator runs in real time since we perform the exact number of ticks per second such that the simulator time advancement amounts to exactly the time passed in real life. We say that the in-simulator time has propagated by the same time horizon with respect to real time.

• If $ρ < 1$ the in-simulator time propagates more slowly than real time, in fact, if $ρ = 0$ the simulator may be completely halted.

• If $ρ > 1$ the in-simulator propagates faster with respect to real time. This is particularly of interest when conducting large simulation studies.

It is convenient to fix $TAPT$ and leave $tps$ unrestricted such that $ρ$ is limited only by the processor performance of the computer running the simulator. If TAPT is chosen too large, say, 10 second the simulator is degraded in its abilities to capture details dictated by the action rules, however the resulting speed up can be very large. If TAPT is chosen small there might be loops without any action and loss of speed up.

Assuming that an elevator moves at a speed $v=1 m/s$, and thus about a floor per 5 seconds and that arrivals occur at the level of seconds then a good choice for $TAPT$ could be 1 s/tick.

Visualization

The depiction of all simulator objects onto the screen is also called rendering. Rendering can be used to asses, visually, whether or not the program behaves as expected. A correct visualization must depict the simulator following a one-to-one correspondence with real life metrics.

If we assume that one meter in real world corresponds to 4 units in the screen, for example, 4 pixels, ie, $PPM=4 pixels/m$ then the advancement per tick of an elevator on the screen corresponds to: