DM825 - Introduction to Machine Learning
Sheet 10, Spring 2011
[pdf format]
|
Exercises 1.29, 1.30, 14.3, 14.1, 14.6, 14.11 of [B1].
Check exercise 14.11. Here is the vresion from the Errata Corrige:

1 Exercise 1 – Tree based methods
You are given the following data points: Negative: (-1, -1) (2, 1) (2,
-1); Positive: (-2, 1) (-1, 1) (1,-1). The points are depicted in
Figure 1.
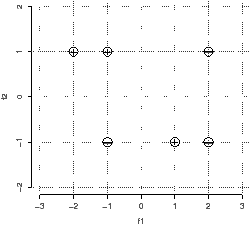
| Figure 1: The data points for classification. |
-
Construct a decision tree using the greedy recursive
bi-partitioning algorithm based on information gain described in
class. Use both criteria the Gini index and the entropy. In the
search for the split threshold θ discretize the continue scale
of the two features and consider only values in {−1.5,0,1.5} for
f1 and {0} for f2. Represent graphically the tree
constructed and draw the decision boundaries in the Figure 1.
Table 1 might be useful for some computations
|
x | y | −(x/y) · log(x/y) | x | y | −(x/y) · log(x/y) |
|
1 | 2 | 0.50 | 1 | 5 | 0.46 |
|
1 | 3 | 0.53 | 2 | 5 | 0.53 |
|
2 | 3 | 0.39 | 3 | 5 | 0.44 |
|
1 | 4 | 0.50 | 4 | 5 | 0.26 |
|
3 | 4 | 0.31 | | | |
| Table 1: Numerical values for the computation of
information gains. |
- Use the tree to predict the outcome for the new point (1,1).
2 Exercise 2 – Nearest Neighbor
- Draw the decision boundaries for 1-Nearest
Neighbor on the Figure 1. Make it accurate enough so that it
is possible to tell whether the integer-valued coordinate points in
the diagram are on the boundary or, if not, which region they are in.
- What class does 1-NN predict for the new point: (1, 1).
- What class does 3-NN predict for the new point: (1, 0).
