Week 50

Lecture Tuesday (08.12.2009)

The ninth lecture will discuss lazy evaluation, infinite data structures, and I/O in Haskell.

Topics

lazy evaluation, infinite structures, IO monad

Reading

Lecture Notes in Blackboard (Course Documents)

Exercise Wednesday (09.12.2009)

1) Define a data structure Set for sets of integers with the constructors Insert and EmptySet. Do not use built-in types (such as [a]) in the definition.

Implement the following functions on this data strucure Set and also give their respective type declarations:

• The function memberSet takes an element x and a set s and returns True if, and only if, x is an element of s.
• The function subSet takes two sets s1 and s2 and returns True if, and only if, s1 is a subset of s2.
• A graph can be represented by a set of edges, i.e., by values of the type Set (a, a). The function hasPath applied to two nodes m and n and a graph g returns True if, and only if, there is a path from m to n in g.
  For example, in the graph Insert (1,2) (Insert (2,3) EmptySet) there is a path from 1 to 3, but not from 3 to 1.

2) Define a higher-order function remove :: (a -> Bool) -> [a] -> [a]. The expression keep f xs should return a list with those elements x of the list xs for which f x evaluates to False.
For example, the expression keep (\x -> x > 23) [23,42] must evaluate to the list [23].

3) Define a higher-order function mapF that take a list of function [f1, f2, ..., fk] and a value x and return the list [f1 x, f2 x, ..., fk x].
For example, the expression mapF [(*3),\x -> x - 2] 5 should return the list [15,3].

4) Consider the following data structure for binary trees:

data BinTree a = Nil | Node (BinTree a) a (BinTree a)

Write functions mapTree :: (a -> b) -> BinTree a -> BinTree b and foldTree :: (b -> a -> b -> b) -> b -> BinTree a -> b that work on BinTree in the same way that map and fold work on (pre-defined) lists.

Use mapTree to implement a function that takes a tree of strings and computes a tree of integers where each node of the new tree contains the length of the string in the corresponding node of the original tree.

Use foldTree to implement a function that takes a tree of integers and returns the sum of the squares of all elements.

Exercise Thursday (10.12.2009)

1) Look at the function take and from, which take some elements from a list and create a list, respectively.

take :: Int -> [a] -> [a]
take 0 xs = []
take (n+1) (x:xs) = x:take n xs

from :: Int -> [Int]
from n = n:from (n+1)

Show every step in the (lazy) evaluation of the expression take 3 (from 8).

2) To represent graphs we can use finite lists of pairs of nodes. Each pair represents an edge between two nodes:

type Graph a = [(a,a)]

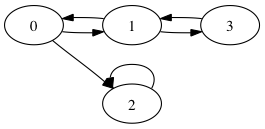
Consider the graph g over integers above. A representation of g as an object of type Graph Int could be:

[(0,1),(1,3),(3,1),(0,2),(1,0),(2,2)]

The following data structure represents trees where every node may have an arbitrary number of children:

data Tree a = Node a [Tree a]

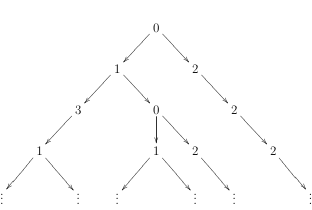
Consider the tree t above that is the result of unfolding the graph g starting from 0. A representation of the first four layers of the infinite tree t as an object of type Tree Int in Haskell could be:

Node 0 [Node 1 [Node 3 [Node 1 [..., ...]], Node 0 [Node 1 [..., ...], Node 2 [...]], Node 2 [Node 2 [Node 2 [...]]]

Implement the following functions in Haskell:

• The function unfold takes a graph g and a node x and returns the tree which results from unfolding g starting from x. Note that for a cyclic graph, the tree can be infinite.
• The function pruneTree :: Tree a -> Int -> Tree a takes a tree t and an integer n and returns the first n layers of the tree. This corresponds to the function take on lists. For example, the expression pruneTree (unfold [(0,1),(1,3),(3,1),(0,2),(1,0),(2,2)] 0) 4 should evaluate to the expression Node 0 [Node 1 [Node 3 [Node 1 []], Node 0 [Node 1 [], Node 2[]]], Node 2 [Node 2 [Node 2 []]].

3) The two functions fibs1 and fibs2 compute the infinite list of Fibonacci numbers starting from 0 and 1, i.e., the list [0,1,1,2,3,5,8,13,21,34,55,...]. The Fibonacci sequence fib₀, fib₁, ... is defined by fib₀ = 0, fib₁ = 1, and fib_n+2 = fib_n+1 + fib_n.

fibs1 = map fib [0..] where
    fib 0 = 0
    fib 1 = 1
    fib (n+2) = (fib (n+1)) + (fib n)

fibs2 = map fib [0..] where
    fib n = fib' n 0 1 where
        fib' n a b | n == 0 = a
                   | True   = fib' (n-1) (a+b) a

Analyze the complexity of evaluating the two expressions take n fibs1 and take n fib2 depending on n. Give upper bounds using the O-notation that are as low as possible. Here, you can assume that addition has constant complexity, i.e., evaluating n + m is in O(1).

Implement a function fibs3 which computes the same list as fibs1 and fibs2 by using a cyclic data structure. Analyze the complexity of evaluating take n fibs3 depending on n as before.

To measure the amount of reductions, in hugs you can type :s +s to switch on the "profiler". This might give you an idea of the behaviour for different n.