DM813 Mandatory Assignment 2: Cophylogenetics
Biological Background
Coevolutionary systems like hosts and their parasites or plants and insects that feed or breed on these plants are commonly used model systems for evolutionary studies. One central aspect in the study of these systems is the evolutionary history of the relations between the two involved groups of species. Often it is possible to determine the phylogeny of each group of species (e.g., the parasite species and the host species) using genetic or morphological data. The current relations between the species from both groups (e.g., which parasite lives on which host species) are often known from field studies or laboratory experiments. An interesting problem is then to reconstruct the common history from the known phylogenies and the current relationships (cmp. Lecture on Cophylogenetics and the corresponding material in the Blackboard System). As presented in the lecture, one approach to solve this problem is to use an evolutionary model that describes the set of possible events that can happen during the coevolution and to assign costs to every event. The problem is then to find a minimum-cost history. Such methods have been called event-based methods. CoRe-PA is a tool for reconstructing the coevolutionary history of host parasite systems that you have to use for this assignment.
In the first part of this assignment you have only to use CoRe-PA and do randomization tests for given host parasite systems to analyze the likelihood of coevolution. In the second part you have to implement an algorithm to solve an problem that has to be solved for drawing two given binary phylogenetic trees and their leaf node associations side-by-side with a minimal number of edges crossing
First Part
You should perform a cophylogenetic analysis with CoRe-PA following
the approach presented in [2]. A tutorial of how of to use CoRe-PA,
including a description of how to make the statistical tests necessary
and how to visualize the results via a boxplot can be
found here
(see Reference [3]). You can chose the tanglegram to be used for your
analysis. However using the same tanglegrams as used in [2] is not
acceptable. A number of original articles is provided in the Blacboard
System (filename: articles.tgz). It is however probably
easier to make your analyis for an example from [4] (IMADA library in
the shelf for DM813). The results of your analysis should in any case
include the best cost vector found, the value of your optimization
criteria (denoted by qc in [2]), the number of events for
each of the four possible events, a figure of the best reconstruction
found, a boxplot of the results of the 100 randomized test instances
(one boxplot for each of the four randomization method, cmp. Figure 5
in [2]), a discussion of your results if you would say that evidence
for cophylogenetic evolution exists (try to use the probability, that
a randomized instance leads to a reconstruction with an equal number
or more coevolutionary events (respectively to reconstructions with a
smaller qc) denoted by pco,>,
pco,≥ (respectively pqu), cmp. Table 1 in
[2]). Note that you need to compute 100 reconstructions for each
boxplot. If your trees are rather large (>40 leaf nodes) computing one
reconstruction based on 2500 Nelder Mead optimizations or 100000
randomly chosen cost vectors can take a few minutes. Do not start with
this analysis too close before the submission deadline!
Second Part
Given two binary phylogenetic trees of a host-parasite system and their corresponding leaf node associations, it is useful to compare them by drawing a tanglegram as it is done for generating the input data for CoRe-PA. We would like to arrange the trees to minimize the number of crossings k induced by the host-parasite associations. This problem is known as the NP-hard Tanglegram Layout problem. Recently a paper presented an easy approach that can solve the problem in an elegant way. An instance of the layout problem to be solved is transformed into a instance of the so-called Balanced Subgraph Problem, and the solution to that problem is then transformed back to a solution of the original problem. The method is described in detail in [1]. In [1] you will also find the example given below.
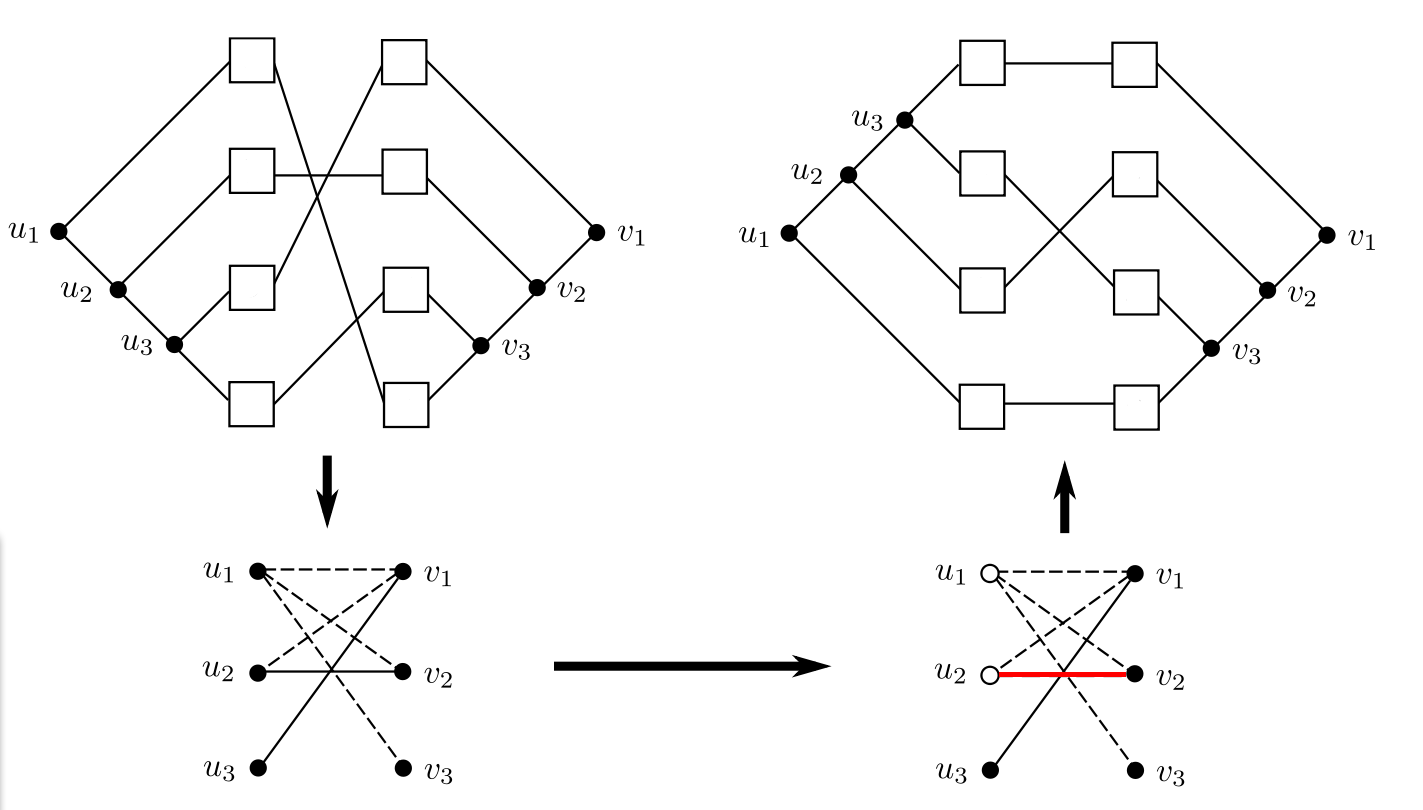
Given are a binary host tree H, a binary parasite tree P and their leaf node associations. This input, called tanglegram, is transformed into an instance of the Balanced Subgraph problem, i.e., into an undirected graph G where all edges are dotted or solid. Note, that this graph may contain multiple edges between two vertices - also multiple edges of the same type can occur, which can be modelled by using integer values as weights for the edges, that correspond to the multiplicity of the corresponding edge. Let G be a bipartite graph with vertex set V , where the vertices in VH (or VP ) correspond to all inner vertices of H (or P , respectively). For each pair (h, h') of leaf nodes in VH with h ≠ h', we will consider all possible pairs of association ((h,p),(h',p')) of the tanglegram with p ≠ p' . Note that there may be several association pairs for one pair (h,h'). For each association pair ((h,p),(h',p')) an edge is drawn between the vertices corresponding to the lowest common ancestors lcaH(h,h') and lcaP(p,p'). For each such edge we test whether there is a crossing between edges (p,h) and (p',h') in the current tanglegram. If so, we draw a solid edge, if a crossing occurs we draw a dotted edge. This graph is used as an instance of the Balanced Subgraph Problem. We try to find an optimal two-coloring of the vertices of G, such that the vertices incident to solid edges have the same color, whereas those incident to dotted edges have different colors, while at the same time, removing as few edges as possible. This corresponds to leaving as few crossings as possible in the tanglegram: The optimal tanglegram is obtained by picking one of the colors, say white, and switching all inner vertices in H and P which correspond to white vertices in G. In the Figure below (adapted from [1]) this procedure is illustrated. In the example it is not possible to find a two-coloring of the graph G without removing (at least one) edge. However if an edge (the red one) is removed, a two coloring becomes possible.
Implementation
Framework for Development
We provide you with a modified version
of CoRe-PA,
in which the necessary stubs (and more) for the implementation you
have to implement are already available. CoRe-PA is provided as
a zip-file, that can be imported as a project in the
Eclipse framework. As CoRe-PA is
an Eclipse
Application, we strongly recommend that you use the Eclipse
Framework for developing. CoRe-PA requires you to use the Eclipse
Platform in version 3.5.1 (Galileo), which is installed on the
IMADA pool machines. You can also download Eclipse Classic 3.6.1 (162
MB) 32bit version for Linux
from here. Note, that
if you do not use the IMADA version of eclispe, you might need to
fix some dependencies to get CoRe-PA running (see below).
CoRe-PA
The project to be imported in the Eclipse Framework for the modified version of CoRe-PA can be found in the Blackboard System (filename core-pa_0.3a_workspace.zip) as a zip file. We will provide a version that is ready for development under Linux and Windows. This version should also be ready to use for development on the IMADA pool machines. The projects that will be provided also include the necessary 32bit GLPK libraries (Linux as well as Windows, see below), but not the necessary Gurobi (see also below) libraries. To import and run CoRe-PA proceed as follows:
- Start Eclipse
- Import > General > Existing Project into Workspace
- Select archive file: take the file core-pa_0.3a_workspace.zip from the Blackboard System and import the workspace.
- In the CoRe-PA project, double-Click "cophylogency products"
- This step only applies, if you work with an Eclipse version that is newer than the version on the IMADA pool machines (for example if you downloaded version 3.6.1 (Helios)). In that case select the tab "Dependencies", enable the option "include optional dependencies when computing required plug-ins", and then "Add required Plug-ins". After that switch back to the "Overview" tab.
- Press "Launch an Eclipse application" (CoRe-PA should start in a new window)
- Create a new Project within the CoRe-PA application (not in Eclipse): File > New Project, name it for example DM813
- Right-Click on DM813 and create for example a Random Nexus File (New > Random Nexus File)
- If you press the button left to "Select tree mode" that looks like three colored boxes, then the method
recalculateNodeOrderfrom fileCoRe-PA/src/com/wieseke/cptk/input/layout/LayoutFormatter.javais executed. If the libraries for GLPK are set correctly inCoRe-PA/src/com/wieseke/cptk/input/layout/LayoutFormatter.java, you should see how in the root node of the host tree the order of the two children is swapped, and the tree is redrawn.
Optimizer
As described above you first have to create an instance of the Balanced Subgraph Problem based on the tanglegram, and then the Balanced Subgraph Problem has to be solved: a minimal number of edges has to be removed from the graph G such that it becomes two-colorable in the way as described above. This optimization problem can of course be solved in many ways. However, whatever possibility you choose, it should be sufficient to only modify the file CoRe-PA/src/com/wieseke/cptk/input/layout/LayoutFormatter.java to do all the implementation work. Note that we already provide the source code of how to solve the specific optimization problem instance underlying the Figure given above with glpk-java (the recommended approach).
- Brute Force Approach:(probably the worst performing approach). If your graph is not two-colorable, then iteratively try to remove all edges individually, and check if the resulting graph is two-colorable. If this is not possible, then try each possible pair of edges, then all possible triple of edges, and so on. Of course this approach will fail due to the immense computation time if the number of edges to be removed gets large. Note that there are easy methods how to improve this approach. For example if two nodes are connected by a solid and a dotted edged, then one of both edges has to be removed. Another example is the following: If there exist several identical edges (which is identical to an edge with a weight >1) between two nodes, then it does not make sense to remove only a part of theses edges.
- GLPK Approach: (recommended)
The GLPK (GNU Linear
Programming Kit) is a callable library that can be used so solve
linear programming (LP), mixed integer programming (MIP), and other
related problems. Formulations of Balanced Subgraph Problems using the
GNU MathProg modeling language can be found in the Blackboard System
(filename
tangle.modandtangle2.mod). The integer programming problem described in the first file corresponds to the example discussed above (from [1]). Withglpsol -m tangle.modyou can solve the problem (glpk is installed on the IMADA pool machines). If you follow this recommended approach you have again the choice: 1.) (not recommended) either you create for each instance to solve a modified version oftangle.mod(in GNU MathProg modeling language format), solve the optimization problem via a system call from Java and read (and parse) the output file fromglpsolthat can be created by using the-ooption. The solution can then be used to draw your optimized layout; or 2.) (recommended) you use the glpk-java Interface directly to solve the Linear Integer Programming problem. Note that it is still a very good idea to understand the linear programming descriptions provided intangle.modandtangle2.modbefore you implement the solution using this approach. As mentioned above, a Java implementation of how to solve the optimzation depicted above is already included in the file CoRe-PA/src/com/wieseke/cptk/input/layout/LayoutFormatter.java of the CoRe-PA project. This also includes the code necessary to load the required libraries. - Gurobi
Approach: Gurobi is a
state-of-the-art linear and mixed integer programming solver that can
be accessed through a Java interface (a comparison showing the
brilliant performance can be
found here). Although Gurobi is
commercial it is free for academic use. However note, that Gurobi will
always require that i.) you are working on a machine that has an IP
address from a university network, and ii.) that you update the Gurobi
license every 7 days via a command line tool. First, you have to
request for an account and download Gurobi (which is very
easy). Gurobi includes many examples of how to use it. If you follow
this approach you again have the choice (similar as in the GLPK
approach). Either (not recommended) you use an external file that
describes the Integer Programming problem, or (recommended) you
implement the optimization directly in Java (not accessing a separate
file for the problem description). For the first possibility, you
should check the example file called
Mip2.javawhich can also be found here. The sample Java code reads a MIP model from a file and solves it. The input file to be read has to be in the so-called Fixed MPS format. Using (a per instance modified version of)tangle.modyou can create an input file using the commandglpsolfrom the GLPK. More precisely you can create an input file in Fixed MPS format based ontangle.mod(which is in the GNU MathProg modeling language format, to be found in the Blackboard System) by the commandglpsol -m tangle.mod --check --wmps tangle.mps. Note that in Gurobi you don't have to parse a result file, but you can access the optimal values for the node colors, and the information which edges to remove, directly from Java. The second option (recommended if you follow the Gurobi approach) is to use the Gurobi Java Interface directly. For this we provide a Java program that solves the instance from the Figure given above (file MipTangle.java in the Blackboard system). Of course this also induces that you do not have to parse an output file. - Any Other Approach: Feel free to come up with any own ideas how to solve that part. Note that for example in this paper the authors use sophisticated techniques to improve the runtime for solving Balanced Subgraph Problem. Hüffner et al. present a method with runtime O(2k m2) time, where k is the number of edge labels violated in an optimal solution and m is the number of graph edges.
Report / Submission
This assignment should be done in groups of two people. A group of more than 2 people is welcome, but only acceptable if you justify this clearly (for example if you follow the brute force approach, the GLPK, and the Gurobi approach, and if you compare them. Another possibility would be to include multifurcation handling (i.e. the input trees are not binary, but a parent node can have >2 children). If you plan to have a group of more than 2 students, please let me know as early as possible (but no later than Dec. 3th) and discuss it with me. The submission of the source code has to be supplemented by a write-up (max. 12 pages). The report has to be written in English. The write-up should contain in any case at least:
- A title page (in addition to the title, names, date, and so on, please indicate also all approaches you followed (brute force, GLPK, and/or Gurobi)).
- An introduction.
- A brief description to the cophylogenetic problem you chose for part 1.
- A cophylogenetic analysis (part 1), that includes the best cost vector found, the value of your optimization criteria (denoted by qc in [2]), the number of events for each of the four possible events, a figure of the best reconstruction found, a boxplot of the results of the 100 randomized test instances (one boxplot for each of the four randomization method, cmp. Figure 5 in [2]), a discussion of your results if you would say that evidence for cophylogenetic evolution exists (try to use the probability, that a randomized instance leads to a reconstruction with an equal number or more coevolutionary events (respectively to reconstructions with a smaller qc) denoted by pco,>, pco,≥ (respectively pqu), cmp. Table 1 in [2]).
- A description and discussion of design decisions you made in part 2.
- A discussion on how large the trees have to become such that your method cannot solve the underlying optimization problem in reasonable time. Also discuss the influence of number of edges to be removed for the optimal coloring and the influence on runtime.
- A Figure of a nontrivial tanglegram (before and after layout optimization was applied), that clearly shows that your approach is working.
- A statement of who contributed with what.
- A conclusion.
- References used.
Create the following directory structure on one of IMADAs pool machines
mandatory2/ mandatory2/report/ mandatory2/source/ mandatory2/results/
In the source directory there should be the (well commented) source code of your implementation (you only have to submit the files you changed and added). If you made a lot of changes, then you can also export the Eclipse project and put the resulting archive file (zip format) in this directory. The results directory should contain a README file, in which you briefly describe the tests you made and what files can be found in the corresponding directory. After putting all the data and the report (use pdf file format) to the correct location, change to the directory mandatory2 and type aflever DM813.
I would appreciate if you hand in a printout of your report and of your source code (only if you submit before Dec. 18th, the 12 pages limit applies only to the report and not to the source code). (Department secretaries office).
The strict deadline for submission (electronically) is Thursday, December, 30th, 10:00. Note however that I will only rarely read mail between Dec. 23rd and Jan 3rd., consider submitting before December 23rd.
Useful References
- [1] A faster fixed-parameter approach to drawing binary tanglegrams, Sebastian Böcker, Falk Hüffner, Anke Truss and Magnus Wahlström, ALGO 2009, Volume 5917 in Lecture Notes in Computer Science, pages 38-49.
- [2] A parameter-adaptive dynamic programming approach for inferring cophylogenies. Daniel Merkle, Martin Middendorf, Nicolas Wieseke, BMC Bioinformatics, 2010, 11 (Suppl 1): S60, doi:10.1186/1471-2105-11-S1-S60 (available from within the SDU network)
- [3] CoRe-PA Tutorial.
- [4] Tangled Trees - Phylogeny, Cospeciation, and Coevolution, 2003, edited by Roderic D. M. Page (IMADA book shelf for DM813)
Frequently Asked Questions (FAQ)
- Are we allowed to work in groups?
Yes, you can (but don't have to) work in groups. A group of more than 2 people is welcome, but only acceptable if you justify this clearly (for example if you follow the brute force approach, the GLPK, and the Gurobi approach, and if you compare them. Another possibility would be to include multifurcation handling (i.e. the input trees are not binary, but a parent node can have >2 children). If you plan to have a group of more than 2 students, please let me know as early as possible (but no later than Dec. 4th) and discuss it with me.