Preliminary version of DM840 Required Assignment 2: Option 1 : Atom-Atom Mapping (changed expected for Option 2)
In the second option for this assignment, your task is to find possible chemical reactions between sets of molecules. You are given a set of educts and a set of products in SMILES notation and your task is to infer all possible graph grammar rules. 90% of all chemical reactions have a so-called mono-cyclic transition state. In the following Figure the reaction for the equilibrium system {ethyl acetate, water} {ethanol-acetic, acid}, with hydrogen chloride as a catalyst is illustrated.
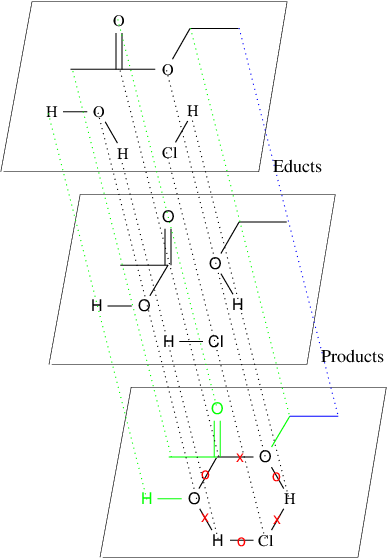
The mapping from the atoms in the educts to the atoms in the products is chosen as above. In general however, there might be different mappings that lead to different Graph Grammar rules. A mapping needs to fulfill certain constraints which can easily be explained by a transition state graph as illustrated above. Based on a given mapping, some bonds remain unchanged, some from the set of educts are removed, and some bonds from the set of products are formed. In the transition state graph above these edges are either unlabeled, or labeled by "X" for a removal of a bond, or by "O" for forming an new bond. Note, that changing a double bond to a single bond is also a removal of a bond, and changing a single bond to a double bond also forms a new bond.
The mono-cyclic reaction above leads to a sequence of adjacent edges in the transition state graph that are alternating labeled with "X" and "O".
We say a mapping is chemically valid, if the labeled edges define one simple cycle graph with alternating labels "X" and "O". It is obvious that in the case of cycles the alternation only allows for cycles of even length. Mappings that lead to more than one cycle are not allowed.
Obviously a Graph Grammar rule can be defined based on such a chemically valid mapping. The straight-forward approach is to put all the nodes of the cycle in context of a graph grammar rule, and define the left- and right-hand side of the graph grammar rule based according to the change of the edge labels. This might create very general rules. Therefore we introduce a parameter k, that can force atoms and edges to be in the context of a rule as follows: If a node has a distance smaller or equal to k to one of the nodes of the found cycle, then that node is also put into the context of the graph grammar rule. All unchanged edges incident to two nodes in the context are then also put into the context. In the example above (bottom figure) the rule generated for k=0 is illustrated in black, the additional nodes and edges in the context for the rule generated for k=1 are depicted in green (note the invisible green carbon atom).
Of course there are, in general, several different chemically valid mappings. Note, that a pair of different mappings might either lead to an identical graph grammar rule, or to a different graph grammar rule (cmp. automorphism groups that we discussed in the context of (sub-)graph isomorphism algorithms that were discussed in the lecture).
Requirements
In a first step you have to define mathematically what a chemically valid mapping is. In the second step you have to enumerate all graph grammar rules based on chemically valid mappings for a set of educts and products and for different values k (context size) and c (cycle length).
Attacking the Problem
The overall goal is enumerate all different Graph Grammar rules based on chemically valid mappings (and create a GML file for each of them if it's not too many) based on specific values k, c, and molecules given in SMILES notation. You are most welcome to use any programming language of your choice. We however provide you a template program in C++ that should (without and specific C++ knowledge) be easily extensible. This program takes care of the GML file generation and also performs the check for identical rules. The part that you need to provide is an (most likely backtracking) algorithm that, more or less cleverly, enumerates all chemically valid graph grammar rules.
All files you need are provided in the
directory /home/daniel/dm840/assignment2/. The files are
more or less self-explanatory. The only file that you need to modify
is the file main.cpp, within that file you basically only
need to change the part between the lines // WORK AREA:
START and // WORK AREA: END. Currently, the source
code includes three different hard-coded mappings from the nodes of
the educt molecule(s) to the nodes of the product molecule(s). Two of
the mappings lead to the same rule. If you execute the compiled
program ./test the program prints out the all nodes, all
edges, and all labels of nodes and edges from the "educt graph" (which
might consist of several components) and for the product
graph. Furthermore it prints out all mappings, and indicates that an
identical rule was found. Note that ./test requires the
directory out to exist. Furthermore note, that you can
execute the program with a file as an argument: mod -f
test.py. The files test.py is also
self-explanatory. If you use the -f option, you don't
have to recompile your file if you want to change the input
compounds. The program will write all created rules on the
console. You can also use the ./wrapper.sh script to
create the summary.
In addition, note the following:
- The context that is created for a rule is based on the mapping
that you use for creating the rule: If you put all the atoms of the
educt as well as the product graph in the mapping, then all atoms, and
all unchanged edges will be in the context of the rule (in the above
figure the mapping indicated by the black, green, and blue dotted
lines). If you only map the vertices incident to changing edges onto
each-other, then no edge will be in the context of the rule (in the
above figure the mapping indicated by the green dotted lines
only). The parameter k should therefore influence the size of a
mapping
vertexMapthat you put viavertexMaps.push_back(vertexMap)in the set of all mappings. - There is code automatically executed that checks for duplicate
rules. First a rule is created based on a mapping via
*r = createRule(...). This rule is checked against all other rules if it is isomorphic, and deleted if this is the case. The code for that is "generic programming", no need for you to understand the details. - The "chemical" plausibility check for the mappings provided is
very simple. It is, for example, checked if you try to change more
than two edges incident to the same node, or if the number of edges
removed and created is not in balance (see
if(doChemistryCheck) ...inmain.cpp). However, if you create rules that can create dangling edges or has other non-chemical properties, the program might just crash. It is your responsibility to check if a mapping induces a mono-cyclic transition state, and you should make sure that you do not add mappings that do not fulfill this property. - You should be very careful when changing parts of the code that is not meant for modification. Although some of the code is really not meant for modification, we still left it in the example program.
Additional Reading
For nice article that gives a bit more chemical background on the idea of
mono-cyclic reaction, see:
James B. Hendrickson: Comprehensive System for Classification and Nomenclature of Organic Reactions. Journal of Chemical Information and Computer Sciences 37(5): 852-860 (1997)
(you can find this article in blackboard, voluntary reading)
Report / Submission
The report must be short and precise (maximum 10 pages, English language). It must include the following:
- A small introduction.
- A section on the formal definition of a chemically valid mapping and a partial chemically valid mapping that determines the nodes and edges in the context based on the parameter k and c.
- A section that describes your implementation to find all (partial) the necessary valid mappings.
- A result section; it should include a table of the following
form. If you couldn't solve the instance, it should be indicated
clearly. Also give information on how long it took to solve the
instances.
\begin{table}[h] \centering \begin{tabular}{ll|cccc}\\ Educts & Products & $k$ & $c$ & $n$ & $t$\\\hline C=C, C=C & C1CCC1 & 0 & 4 & & \\ C=C, C=C & C1CCC1 & 1 & 4 & & \\ O, Cl, CC(=O)OCC & Cl, OCC, CC(=O)O & 0 & 6 \\ O, Cl, CC(=O)OCC & Cl, OCC, CC(=O)O & 1 & 6 \\ O, Cl, CC(=O)OCC & Cl, OCC, CC(=O)O & 2 & 6 \\ C1C(O)CC(O)C(O)C1 & C=CO, C=CO, C=CO & 0 & 6 & & \\ C1C(O)CC(O)C(O)C1 & C=CO, C=CO, C=CO & 1 & 6 & & \\ CC=CC=CC, OC1C=CC=CC=1 & C=CC=CC=C, OC(=C)C=CC=C & 0 & 6 & & \\ CC=CC=CC, OC1C=CC=CC=1 & C=CC=CC=C, OC(=C)C=CC=C & 1 & 6 & & \\ CC=CC=CC, OC1C=CC=CC=1 & C=CC=CC=C, OC(=C)C=CC=C & 2 & 6 & & \\ CC, OC1C=CC=CC=1 & C=C, OC(=C)C=CC=C & 0 & 6 & & \\ CC, OC1C=CC=CC=1 & C=C, OC(=C)C=CC=C & 1 & 6 & & \\ CC, OC1C=CC=CC=1 & C=C, OC(=C)C=CC=C & 2 & 6 & & \\ OP(=O)(O)OP(=O)(O)O, O & O=P(O)(O)O, O=P(O)(O)O & 0 & 4 & & \\ OP(=O)(O)OP(=O)(O)O, O & O=P(O)(O)O, O=P(O)(O)O & 1 & 4 & & \\ OP(=O)(O)OP(=O)(O)O, O & O=P(O)(O)O, O=P(O)(O)O & 0 & 6 & & \\ OP(=O)(O)OP(=O)(O)O, O & O=P(O)(O)O, O=P(O)(O)O & 1 & 6 & & \\ C\#N, C\#N & N=CC\#N & 0 & 4 & & \\ C\#N, C\#N & N=CC\#N & 1 & 4 & & \\ \end{tabular} \end{table}
Note that the backslash before the triple bond sign is only there because of LaTeX, the SMILES string does not contain it.
In this table the parameters k and c are defined as described above, n is the number of different graph grammar rules you found, and t is the number of different mappings you created in order to find those t different graph grammar rules, i.e., the number of calls tovertexMaps.push_back(vertexMap). - An example that illustrates how an increasing k limits the possibility of applying rules: Given a fixed set of educts and products (you can choose them) infer rule sets Rk for different values of k. Expand the chemical space (initially filled with the educts only) by applying one of the rules of Rk once only (for at least two different values of k). Depict the two different hypergraph, in at least one of them the initially given product set should be a proper subset of the products created by the rule application.
- A section where you discuss how you could speedup your implementation but maybe applying methods similar to the pruning methods in the Ullmann and/or McKay's algorithm.
- In case you work as a group: a paragraph on who contributed with what.
DM840 Required Assignment 2: Option 2 : Graph Isomorphism
In the second option for this assignment your task is to improve code for the canonicalization of a undirected graph. You won't get much guidance and you can freely chose how to optimize, we will only give some recommendation. If you do not have a certain degree of experience with C++ you should be careful to chose this option. You were already provided C++ source code which implements graph canonicalization based on a different search tree exploration (based on individualization applied to equitable partitions), partition refinement, and testing. The code is heavily using concepts from Generic Programming and is therefore heavily templated. Pruning and different tree traversal methods is implemented to a certain degree.
- You should start with properly understanding the code that you are provided.
- Any reasonable extension you want to try out is acceptable. A very
specific suggestion is to proof (!) and implement Lemma 2.25 of the
article by
McKay (nauty). One
of the cases says: in case you have cells of size one or two only in a
partition, you do not need to generate all the children as all of them
will be isomorphic, i.e., branching is not necessary (this case is
implemented already, the two others are not). The only file that you
have to modify from the source code provided in blackboard
is
graph_canon/include/graph_canon/visitor/implicit_automorphism.hpp. - Follow the submission guideline from Option 1.
DM840 Required Assignment 2: Option 3 : Molecule Invariant based on MCB
In
case you prefer not to touch C++ code, you can choose this
option. Implement the computation of the invariant w(G) from the
article "Minimum Cycle Bases and Their Applications" by Franziska
Berger (found in blackboard). We recommend you use the python
interface of mød for that. You can then easily specify a
molecule graph based on a SMILES string and access all vertices and
edges, please refer to the
Graph Interface example. It will very likely also be helpful to use a very powerfull library to manipulate networks and graphs, called NetworkX . You can install this in the terminal room by using the command pip install --user networkx. Your task is to
- Implement an algorithm for finding the Minimum Cycle Basis (we recommend Horton's algorithm). You are allowed to use NetworkX for calculating the shortest paths in a graph. You are not allowed to use
cycle_basisfrom NetworkX. Note, that you cannot directly use the labelled graph frommød, as double and triple bonds need to be multi-edges for the approach described in the paper from Berger. - Based on the MCB implement the inference of the invariant. Make sure, that ypur code calcualtes the invariants for all the examples from Fig. 4 of the paper correctly.
- Add more examples that show the correct implementation of your code.
- Follow the submission guideline from Option 1.
Submission
For submitting the report and the sources proceed as follows: create the following directory structure
assignment2/ assignment2/code/ assignment2/report/ assignment2/results/
Change to the directory assignment2 and type aflever DM840 your@mail.com.
Additionally, you shall hand in a printout of your report (Department secretaries office).
The strict deadline for submission (electronically) is 22.05.2017, 11am. The electronically submitted and the printout version need to be identical.