Week 40

Lecture Monday (1.10.2012)

The eigth lecture will focus on declaring new types and determining the most general type of functions. Then we will learn about higher-order functions.

Topics

type declarations, algebraic data types, higher-order functions, computing most general types

Reading

Lecture Notes in Blackboard (Course Documents)

Lecture Tuesday (2.10.2012)

The ninth lecture will discuss lazy evaluation, infinite data structures, and I/O in Haskell.

Topics

lazy evaluation, infinite structures, IO monad

Reading

Lecture Notes in Blackboard (Course Documents)

Exercise Tuesday (2.10.2012)

1) Give the most general type for the following Haskell functions f, g, and h. Explain your reasoning.

f x y xs z = f z y (x:xs) x

g x = if True then \y -> y else \xs -> x:xs

h [] z r = z ++ r
h (x:y) z r = x ++ h y z r

2) Define a Haskell function append that performs list concatenation, i.e., that behaves like the built-in function (++). You may only use pattern matching and constructors like [] and (:). Give a type declaration with the most general type for append.

Compare your implementation of append to the preceding definition of sum for computing the sum of all elements of the list. What is the most general type of sum? Discuss why certain functions can be defined on polymorphic lists and others cannot.

3) Define a data structure Set for sets of integers with the constructors Insert and EmptySet. Do not use built-in types (such as [a]) in the definition.

Implement the following functions on this data strucure Set and also give their respective type declarations:

• The function memberSet takes an element x and a set s and returns True if, and only if, x is an element of s.
• The function subSet takes two sets s1 and s2 and returns True if, and only if, s1 is a subset of s2.
• A graph can be represented by a set of edges, i.e., by values of the type Set (a, a). The function hasPath applied to two nodes m and n and a graph g returns True if, and only if, there is a path from m to n in g.
  For example, in the graph Insert (1,2) (Insert (2,3) EmptySet) there is a path from 1 to 3, but not from 3 to 1.

4) Define a higher-order function remove :: (a -> Bool) -> [a] -> [a]. The expression keep f xs should return a list with those elements x of the list xs for which f x evaluates to False.
For example, the expression keep (\x -> x > 23) [23,42] must evaluate to the list [23].

5) Define a higher-order function mapF that take a list of function [f1, f2, ..., fk] and a value x and return the list [f1 x, f2 x, ..., fk x].
For example, the expression mapF [(*3),\x -> x - 2] 5 should return the list [15,3].

6) Consider the following data structure for binary trees:

data BinTree a = Nil | Node (BinTree a) a (BinTree a)

Write functions mapTree :: (a -> b) -> BinTree a -> BinTree b and foldTree :: (b -> a -> b -> b) -> b -> BinTree a -> b that work on BinTree in the same way that map and fold work on (pre-defined) lists.

Use mapTree to implement a function that takes a tree of strings and computes a tree of integers where each node of the new tree contains the length of the string in the corresponding node of the original tree.

Use foldTree to implement a function that takes a tree of integers and returns the sum of the squares of all elements.

7) Look at the function take and from, which take some elements from a list and create a list, respectively.

take :: Int -> [a] -> [a]
take 0 xs = []
take (n+1) (x:xs) = x:take n xs

from :: Int -> [Int]
from n = n:from (n+1)

Show every step in the (lazy) evaluation of the expression take 3 (from 8).

Exercise Wednesday (3.10.2012)

1) To represent graphs we can use finite lists of pairs of nodes. Each pair represents an edge between two nodes:

type Graph a = [(a,a)]

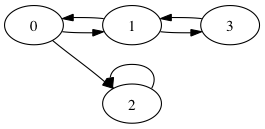
Consider the graph g over integers above. A representation of g as an object of type Graph Int could be:

[(0,1),(1,3),(3,1),(0,2),(1,0),(2,2)]

The following data structure represents trees where every node may have an arbitrary number of children:

data Tree a = Node a [Tree a]

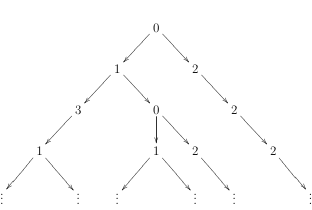
Consider the tree t above that is the result of unfolding the graph g starting from 0. A representation of the first four layers of the infinite tree t as an object of type Tree Int in Haskell could be:

Node 0 [Node 1 [Node 3 [Node 1 [..., ...]], Node 0 [Node 1 [..., ...], Node 2 [...]], Node 2 [Node 2 [Node 2 [...]]]

Implement the following functions in Haskell:

• The function unfold takes a graph g and a node x and returns the tree which results from unfolding g starting from x. Note that for a cyclic graph, the tree can be infinite.
• The function pruneTree :: Tree a -> Int -> Tree a takes a tree t and an integer n and returns the first n layers of the tree. This corresponds to the function take on lists. For example, the expression pruneTree (unfold [(0,1),(1,3),(3,1),(0,2),(1,0),(2,2)] 0) 4 should evaluate to the expression Node 0 [Node 1 [Node 3 [Node 1 []], Node 0 [Node 1 [], Node 2[]]], Node 2 [Node 2 [Node 2 []]].

2) The two functions fibs1 and fibs2 compute the infinite list of Fibonacci numbers starting from 0 and 1, i.e., the list [0,1,1,2,3,5,8,13,21,34,55,...]. The Fibonacci sequence fib₀, fib₁, ... is defined by fib₀ = 0, fib₁ = 1, and fib_n+2 = fib_n+1 + fib_n.

fibs1 = map fib [0..] where
    fib 0 = 0
    fib 1 = 1
    fib (n+2) = (fib (n+1)) + (fib n)

fibs2 = map fib [0..] where
    fib n = fib' n 0 1 where
        fib' n a b | n == 0 = a
                   | True   = fib' (n-1) (a+b) a

Analyze the complexity of evaluating the two expressions take n fibs1 and take n fib2 depending on n. Give upper bounds using the O-notation that are as low as possible. Here, you can assume that addition has constant complexity, i.e., evaluating n + m is in O(1).

Implement a function fibs3 which computes the same list as fibs1 and fibs2 by using a cyclic data structure. Analyze the complexity of evaluating take n fibs3 depending on n as before.

To measure the amount of reductions, in hugs you can type :s +s to switch on the "profiler". This might give you an idea of the behaviour for different n.

3) Implement a function sumList :: IO () in Haskell. If sumList is executed, the user can type in a list of integers on the keyboard in standard Haskell notation. Afterwards, the sum of these integers is printed on the screen using the function putStr. For example, if the user enters the string [1, -5, 70], then the number 66 is displayed on the screen.

In order to convert a String into an [Int] you may use the built-in function read :: String -> [Int]. For example, read "[1, -5, 70]" :: [Int] will read in the list of integers [1, -5, 70].

4) Write a program in Haskell which tells the user to think of a secret integer number. Then the program asks the user for a lower and an upper bound of an interval containing the secret number. Afterwards, the computer tries to guess the secret number and asks the user if its guess is the right one or the secret number is smaller or bigger. The program repeats guessing until it finds the secret number. It should try to use as few guesses as possible.

Here is a successful session (where inputs by the user are enclosed in underscores):

Try to think of a number in a certain range!
Please enter the lower bound of your range: _1_
Please enter the upper bound of your range: _100_
Searching from 1 to 100
My guess #1: 50
Am I (r)ight or is your number (s)maller or (b)igger? _s_
Smaller? Let me see ...
My guess #2: 25
Am I (r)ight or is your number (s)maller or (b)igger? _b_
Bigger? Well, I think ...
My guess #3: 37
Am I (r)ight or is your number (s)maller or (b)igger? _s_
Smaller? Let me see ...
My guess #4: 31
Am I (r)ight or is your number (s)maller or (b)igger? _b_
Bigger? Well, I think ...
My guess #5: 34
Am I (r)ight or is your number (s)maller or (b)igger? _r_
Yes! I made it!

Here is another successful session:

Try to think of a number in a certain range!
Please enter the lower bound of your range: _1_
Please enter the upper bound of your range: _100_
Searching from 1 to 100
My guess #1: 50
Am I (r)ight or is your number (s)maller or (b)igger? _b_
Bigger? Well, I think ...
My guess #2: 75
Am I (r)ight or is your number (s)maller or (b)igger? _s_
Smaller? Let me see ...
My guess #3: 62
Am I (r)ight or is your number (s)maller or (b)igger? _b_
Bigger? Well, I think ...
My guess #4: 68
Am I (r)ight or is your number (s)maller or (b)igger? _b_
Bigger? Well, I think ...
My guess #5: 71
Am I (r)ight or is your number (s)maller or (b)igger? _b_
Bigger? Well, I think ...
My guess #6: 73
Am I (r)ight or is your number (s)maller or (b)igger? _b_
Bigger? Well, I think ...
... it is 74!